【题目】如图,AE∥BF,AC平分∠BAD,交BF于点C,BD平分∠ABC,交AE于点D,连接CD. 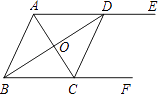
(1)若AB=1,则BC的长=;
(2)求证:四边形ABCD是菱形.
参考答案:
【答案】
(1)1
(2)证明:∵AC平分∠BAD,
∴∠BAC=∠CAD,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠BAC=∠BCA,
∴BC=BA,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵AD∥BC,
∴∠ADB=∠BDC,
∴∠ABD=∠ADB,
∴AB=AD,
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵AB=AD,
∴四边形ABCD是菱形.
【解析】(1)解:∵AC平分∠BAD, ∴∠BAC=∠CAD,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠BAC=∠BCA,
∴BC=BA=1.
所以答案是1.
【考点精析】解答此题的关键在于理解菱形的判定方法的相关知识,掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.
-
科目: 来源: 题型:
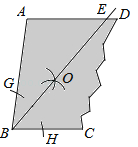
查看答案和解析>>【题目】如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于
 GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.(1)求证:AB=AE;
(2)若∠A=100°,求∠EBC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是我们常见的地砖上的图案,其中包含了一种特殊的平面图形﹣正八边形.
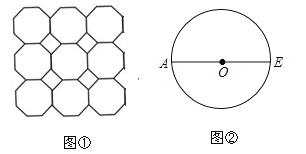
(1)如图②,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹);
(2)在(1)的前提下,连接OD,已知OA=5,若扇形OAD(∠AOD<180°)是一个圆锥的侧面,则这个圆锥底面圆的半径等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一工程,在工程招标时,接到甲,乙两个工程队的投标书.施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲,乙两队的投标书测算,有如下方案: (i)甲队单独完成这项工程刚好如期完成;
(ii)乙队单独完成这项工程要比规定日期多用6天;
(iii)若甲,乙两队合做3天,余下的工程由乙队单独做也正好如期完成.
试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由. -
科目: 来源: 题型:
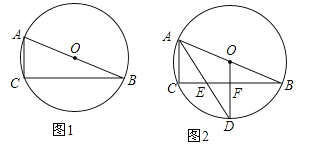
查看答案和解析>>【题目】已知⊙O为△ABC的外接圆,圆心O在AB上.
(1)在图1中,用尺规作图作∠BAC的平分线AD交⊙O于D(保留作图痕迹,不写作法与证明);
(2)如图2,设∠BAC的平分线AD交BC于E,⊙O半径为5,AC=4,连接OD交BC于F.
①求证:OD⊥BC;
②求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】情境观察:
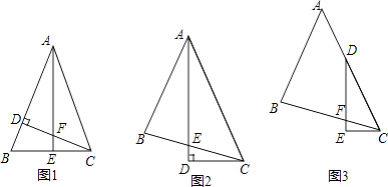
(1)如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F. ①写出图1中所有的全等三角形;
②线段AF与线段CE的数量关系是 .
(2)如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E. 求证:AE=2CD.
(3)如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC= ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE. 要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE. 要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两地有公路和铁路相连,在这条路上有一家食品厂,它到B地的距离是到A地的2倍,这家工厂从A地购买原料,制成食品卖到B地.已知公路运价为1.5元/(公里吨),铁路运价为1元/(公里吨),这两次运输(第一次:A地→食品厂,第二次:食品厂→B地)共支出公路运费15600元,铁路运费20600元.

问:
(1)这家食品厂到A地的距离是多少?
(2)这家食品厂此次共买进原料和卖出食品各多少吨?
相关试题

