【题目】我们运用图(Ⅰ)中大正方形的面积可表示为(a+b)2,也可表示为c3+4(![]() ab),即(a+b)2=c2+4(
ab),即(a+b)2=c2+4(![]() ab)由此推导出一个重要的结论a2+b2=c2,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
ab)由此推导出一个重要的结论a2+b2=c2,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.



(1)请你用图(Ⅱ)(2002年国际数学家大会会标)的面积表达式验证勾股定理(其中四个直角三角形的较大的直角边长都为a,较小的直角边长都为b,斜边长都为c).
(2)请你用(Ⅲ)提供的图形进行组合,用组合图形的面积表达式验证:(x+2y)2=x2+4xy+4y2.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)阴影部分面积由大正方形面积减去小正方形面积,也可以由四个直角三角形面积之和求出,两者相等即可得证;
(2)拼成如图所示图形,根据大正方形边长为x+2y,表示出正方形面积,再由两个小正方形与两个矩形面积之和求出,即可验证.
试题解析:(1)S阴影=4×![]() ab,S阴影=c2-(a-b)2,
ab,S阴影=c2-(a-b)2,
∴4×![]() ab=c2-(a-b)2,即2ab=c2-a2+2ab-b2,
ab=c2-(a-b)2,即2ab=c2-a2+2ab-b2,
则a2+b2=c2;
(2)如图所示,

大正方形的面积为x2+4y2+4xy,也可以为(x+2y)2,
则(x+2y)2=x2+4xy+4y2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是

A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
思路:(1) 作AD⊥BC于D,设BD = x,用含x的代数式表示CD;(2)根据勾股定理,利用AD作为“桥梁”,建立方程模型,求出x;(3)利用勾股定理求出AD的长,再计算三角形面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物
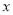 元(
元(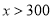 ).
).(1)请用含
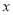 的代数式分别表示顾客在两家超市购物所付的费用;
的代数式分别表示顾客在两家超市购物所付的费用;(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由;
(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?
-
科目: 来源: 题型:
查看答案和解析>>【题目】【题目】如图,两个反比例函数C1:y=
 和C2:y=
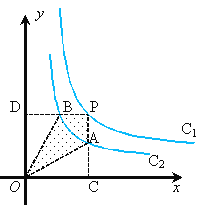
和C2:y= 在第一象限内的图象如图,P在C1上作PC、PD垂直于坐标轴,垂线与C2交点为A、B,则下列结论,其中正确的是( )
在第一象限内的图象如图,P在C1上作PC、PD垂直于坐标轴,垂线与C2交点为A、B,则下列结论,其中正确的是( )①△ODB与△OCA的面积相等;②四边形PAOB的面积等于k1- k2;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点

A. ①② B. ②④ C. ①②④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个反比例函数C1:y=
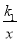 和C2:y=
和C2:y=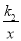 在第一象限内的图象如图,P在C1上作PC、PD垂直于坐标轴,垂线与C2交点为A、B,则下列结论,其中正确的是( )
在第一象限内的图象如图,P在C1上作PC、PD垂直于坐标轴,垂线与C2交点为A、B,则下列结论,其中正确的是( )①△ODB与△OCA的面积相等;②四边形PAOB的面积等于k1- k2;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点
A. ①② B. ②④ C. ①②④ D. ①③④
【答案】C
【解析】①∵A、B两点都在y=
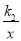 上,∴△ODB与△OCA的面积都都等于
上,∴△ODB与△OCA的面积都都等于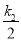 ,则①正确;②S矩形OCPB-S△AOC-S△DBO=|k2|-2×|k1|÷2=k2-k1,则②正确;③只有当P的横纵坐标相等时,PA=PB,错误;④当点A是PC的中点时,点B一定是PD的中点,正确.故选C.
,则①正确;②S矩形OCPB-S△AOC-S△DBO=|k2|-2×|k1|÷2=k2-k1,则②正确;③只有当P的横纵坐标相等时,PA=PB,错误;④当点A是PC的中点时,点B一定是PD的中点,正确.故选C.【题型】单选题
【结束】
10【题目】如图,反比例函数
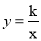 (k>0)与一次函数
(k>0)与一次函数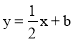 的图象相交于两点A(
的图象相交于两点A(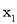 ,
,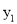 ),B(
),B(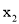 ,
,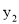 ),线段AB交y轴与C,当|
),线段AB交y轴与C,当|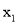 -
-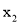 |=2且AC = 2BC时,k、b的值分别为( )
|=2且AC = 2BC时,k、b的值分别为( )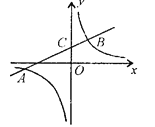
A. k=
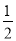 ,b=2 B. k=
,b=2 B. k=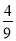 ,b=1 C. k=
,b=1 C. k=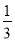 ,b=
,b=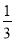 D. k=
D. k=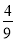 ,b=
,b=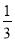
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的长为6,宽为3,点O1为矩形的中心,⊙O2的半径为1,O1O2⊥AB于点P,O1O2=6.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边只有一个公共点的情况一共出现( )

A.3次
B.4次
C.5次
D.6次
相关试题

