【题目】如图,某景区内的环形路是边长为1000米的正方形ABCD.现有1号、2号两辆游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形路连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为200米/分,设行驶时间为t分,解决下列问题:
(1)当0≤t≤10时,分别写出1号车、2号车在左半环线离出口A的路程(用含t的代数式表示);
(2)当0≤t≤10时,求当两车相距的路程是400米时的t值;
(3)当t为何值时,1号车第三次恰好经过景点C?并直接写出这一段时间内它与2号车相遇的次数.

参考答案:
【答案】(1) 200t米, (2000-200t)米;(2) t的值为4或6;(3)这一段时间内它与2号车相遇的次数为5次.
【解析】(1)根据路程=速度×时间结合AB、BC的长度,即可得出结论;
(2)分相遇前和相遇后两种情况找出关于t的一元一次方程,解之即可得出结论;
(3)1号车第三次恰好经过景点C行驶的路程,再由时间=路程÷速度即可求得t的值.
(1)1号车在左半环线离出口A的路程为200t米,2号车在左半环线离出口A的路程为(2000-200t)米;
(2)当相遇前相距400米时,可列方程2000-200t-200t=400,解得t=4;
当相遇后相距400米时,可列方程200t+200t-2000=400,解得t=6.
答:当两车相距的路程是400米时,t的值为4或6.
(3)由题意,得1号车第三次恰好经过景点C行驶的路程为1000×2+1000×4×2=10000(米),所以1号车第三次恰好经过景点C需要的时间为t=10000÷200=50(分);
这一段时间内它与2号车相遇的次数为5次.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,AC,BD是对角线。将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG。则下列结论:
①四边形AEGF是菱形 ②△AED≌△GED
③∠DFG=112.5° ④BC+FG=1.5
其中正确的结论是( )
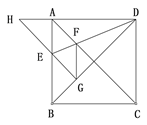
A. ①②③④ B. ①②③ C. ①② D. ②
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.

(1)如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且OM恰好平分∠BOC.此时∠AOM= 度;
(2)如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司以每吨
 元的价格收购了
元的价格收购了 吨某种药材,若直接在市场上销售,每吨的售价是
吨某种药材,若直接在市场上销售,每吨的售价是 元.该公司决定加工后再出售,相关信息如下表所示:
元.该公司决定加工后再出售,相关信息如下表所示:工艺
每天可加工药材的吨数
成品率
成品售价
(元/吨)
粗加工
14
80%
6000
精加工
6
60%
11000
(注:①成品率80%指加工100吨原料能得到80吨可销售药材;②加工后的废品不产生效益.)
受市场影响,该公司必须在
 天内将这批药材加工完毕.
天内将这批药材加工完毕.(1)若全部粗加工,可获利_______________________元;
(2)若尽可能多的精加工,剩余的直接在市场上销售,可获利_____________元;
(3)若部分粗加工,部分精加工,恰好
 天完成,求可获利多少元?
天完成,求可获利多少元? -
科目: 来源: 题型:
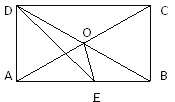
查看答案和解析>>【题目】如图,在矩形ABCD中,DE平分∠ADC, 且∠EDO=15°,则∠OED=________°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列角度化成以度表示的形式.
(1)15°24′36″; (2)36°59′96″; (3)50°65′60″.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个水池深3m,池中水深1m,现在要把水池中的水注满,每注水1h,池中的水深增加0.4m.
(1)写出池中的水深y(m)与注水时间x(h)之间的函数关系式.
(2)求自变量的取值范围.
(3)画出这个函数的图像.
相关试题

