【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() 于点
于点![]() 交
交![]() 于
于![]() 点,延长
点,延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() .
.

(1)证明:四边形![]() 是矩形;
是矩形;
(2)当![]() 时,猜想线段
时,猜想线段![]() 、
、![]() 、
、![]() 的数量关系,并证明.
的数量关系,并证明.
参考答案:
【答案】(1)详见解析;(2)![]() ,证明详见解析
,证明详见解析
【解析】
(1)根据平行四边形的性质得到AD∥BC,AD=BC,进而求出AD=FH,再根据平行四边形的判定得出四边形AFHD是平形四边形,最后根据矩形的判定得出即可得到答案;
(2)根据平行四边形的性质得到AB∥CD,求出∠1=∠3,推出AE=AD,再根据正方形的判定和性质得出AD=DH,求出△DAG≌△DHM,最后根据全等三角形的性质得出∠2=∠3=∠HDM,∠AGD=∠M,求出∠M=∠CDM即可得到答案.
(1)∵四边形![]() 是平行四边形
是平行四边形
∴![]() ,
,![]() (平行四边形对边平行且相等),
(平行四边形对边平行且相等),
∵![]()
∴![]() ,
,
∴![]() (等量替换),
(等量替换),
∴四边形![]() 是平行四边形(对边平行且相等的四边形是平行四边形),
是平行四边形(对边平行且相等的四边形是平行四边形),
∵![]() ∴
∴![]() ,
,
∴平行四边形![]() 是矩形;
是矩形;
(2)猜想:![]()
证明:如图,延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() ,
,

∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ∴
∴![]() ,
,
∵![]() 平分
平分![]() ∴
∴![]() ∴
∴![]() ∴
∴![]() ,
,
∵![]() ∴
∴![]() ,
,
∴四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
在△DAG和△DHM中,

∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
-
科目: 来源: 题型:
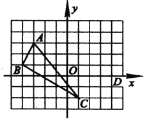
查看答案和解析>>【题目】在平面直角坐标系中, △ABC三个顶点的位置如图(每个小正方形的边长均为1).
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′、B′、C′三点的坐标: A′(_____,______); B′(_____,______); C′(_____,______)。
(3)求△ABC的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展、体育特长、艺术特长和时间活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题.
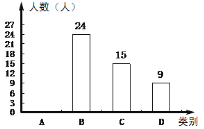
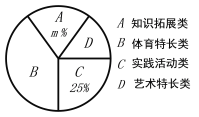
(1)求扇形统计图中的m的值,并补全条形统计图;
(2)已知该校800名学生,计划开设“实践活动类”课程,每班安排20人,问学校开设多少个“实践活动课”课程的班级比较合理.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数
众数
中位数
方差
甲
8
8
0.4
乙
9
3.2
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y1=ax2+2x+c与直线y2=kx+b交于点A(-1,0)、B(2,3).
(1)求a、b、c的值;
(2)直接写出当y1<y2时,自变量的范围是__________________________.
(3)若点C是抛物线的顶点,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形
 的周长为
的周长为 ,两个邻角
,两个邻角 与
与 的比是
的比是 ,则这个菱形的面积是__________.
,则这个菱形的面积是__________.
相关试题

