【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
参考答案:
【答案】(1)根据平行四边形的性质可得AB∥CD,AB=CD,根据平行线的性质可得∠B=∠BCF,由E是BC的中点可得BE=CE,再结合对顶角相等可证得△ABE≌△FCE,问题得证;
(2)由AB=CD,AB=CF结合AD=2AB可证得AD=DF,再根据等腰三角形的性质即可作出判断.
【解析】试题分析:(1)由在ABCD中,E是BC的中点,利用ASA,即可判定△ABE≌△FCE,继而证得结论;(2)由AD=2AB,AB=FC=CD,可得AD=DF,又由△ABE≌△FCE,可得AE=EF,然后利用三线合一,证得结论.
试题解析:(1)∵四边形ABCD是平行四边形, ∴AB∥DF, ∴∠ABE=∠FCE, ∵E为BC中点, ∴BE=CE,
在△ABE与△FCE中,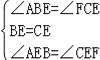 , ∴△ABE≌△FCE(ASA), ∴AB=FC;
, ∴△ABE≌△FCE(ASA), ∴AB=FC;
(2)∵AD=2AB,AB=FC=CD, ∴AD=DF, ∵△ABE≌△FCE, ∴AE=EF, ∴DE⊥AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值小于3的负整数是 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)24+(-14)+(-16)-(-8)

(2)(-24)×(
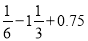 );
);(3)
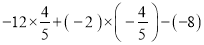 ;
;(4)
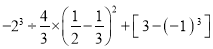
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(2,a)与点B(b,3)关于x轴对称,则a+b的值为( )
A.﹣1B.1C.2D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x﹣1)2+3的对称轴是( )
A.直线x=1
B.直线x=3
C.直线x=﹣1
D.直线x=﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=

 ﹣
﹣ x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.(1)求点A和点B的坐标;
(2)求证:四边形DECF是矩形;
(3)连接EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=3x2向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )
A.y=3(x﹣1)2﹣2
B.y=3(x+1)2﹣2
C.y=3(x+1)2+2
D.y=3(x﹣1)2+2
相关试题

