【题目】把下列各式分解因式:
(1)4x3-6x2;
(2)2a2b+5ab+b;
(3)6p(p+q)-4q(p+q);
(4)(x-1)2-x+1;
(5)-3a2b+6ab2-3ab.
参考答案:
【答案】(1)2x2(2x-3);(2)b(2a2+5a+1);(3)2(p+q)(3p-2q);(4)(x-1)(x-2);(5)-3ab(a-2b+1).
【解析】
(1)直接利用提取公因式法,提取公因式2x2,进而分解因式得出答案;
(2)直接利用提取公因式法,提取公因式b,进而分解因式得出答案;
(3)直接利用提取公因式法,提取公因式2(p+q),进而分解因式得出答案;
(4)直接利用提取公因式法,提取公因式(x﹣1),进而分解因式得出答案.
(5)直接利用提取公因式法,提取公因式﹣3ab,进而分解因式得出答案.
(1)原式=![]() =
=![]() ;
;
(2)原式= b2a2+ b5a+ b1=b(2a2+5a+1);
(3)原式=2(p+q)3p-2(p+q)2q=2(p+q)(3p-2q);
(4)原式=(x-1)2-(x-1)=(x-1)(x-1-1)= (x-1)(x-2);
(5)原式=-3aba+(-3ab)(-2b)+(-3ab)1=-3ab(a-2b+1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
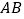 、
、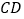 相交于点
相交于点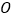 ,
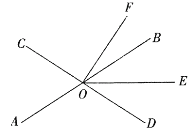
,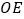 平分
平分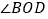 .
.
(1)若
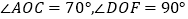 ,求
,求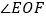 的度数;
的度数;(2)若
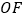 平分
平分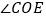 ,∠BOF=12°,若设∠BOE=x°.
,∠BOF=12°,若设∠BOE=x°.①则
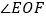 = . (用含
= . (用含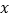 的代数式表示)
的代数式表示)②求
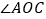 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线
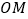 上有三点
上有三点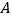 、
、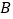 、
、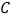 ,满足OA=30cm,AB=90cm,BC=15cm,点
,满足OA=30cm,AB=90cm,BC=15cm,点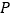 从点
从点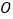 出发,沿
出发,沿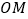 方向以
方向以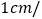 秒的速度匀速运动,点
秒的速度匀速运动,点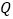 从点
从点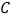 出发在线段
出发在线段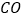 上向点
上向点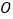 匀速运动,两点同时出发,当点
匀速运动,两点同时出发,当点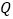 运动到点
运动到点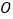 时,点
时,点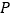 、
、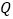 停止运动.
停止运动.(1)若点
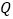 运动速度为
运动速度为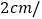 秒,经过多长时间
秒,经过多长时间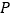 、
、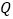 两点相遇?
两点相遇?(2)当
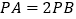 时,点
时,点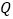 运动到的位置恰好是线段OB的中点,求点
运动到的位置恰好是线段OB的中点,求点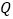 的运动速度;
的运动速度;(3)当点
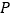 运动到线段
运动到线段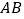 上时,分别取
上时,分别取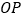 和
和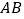 的中点
的中点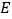 、
、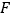 ,求
,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】六一期间,某公园游戏场举行“迎奥运”活动.有一种游戏的规则是:在一个装有6个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为40000人次,公园游戏场发放的福娃玩具为10000个.
(1)求参加一次这种游戏活动得到福娃玩具的概率;
(2)请你估计袋中白球接近多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,操场的两端为半圆形,中间是一个长方形. 已知半圆的半径为r,直跑道的长为l,请用关于r,l的多项式表示这个操场的面积. 这个多项式能分解因式吗?若能,请把它分解因式,并计算当r=40m,l=30πm时操场的面积(结果保留π);若不能,请说明理由.
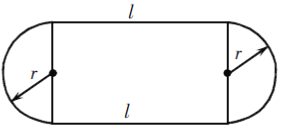
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个暗箱里放有a个除颜色外都完全相同的红、白、蓝三种球,其中红球有4个,白球有10个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在20%.
(1)试求出a的值;
(2)从中任意摸出一个球,下列事件:①该球是红球;②该球是白球;③该球是蓝球.试估计这三个事件发生的可能性的大小,并将三个事件按发生的可能性从小到大的顺序排列(用序号表示事件). -
科目: 来源: 题型:
查看答案和解析>>【题目】下表记录了一名球员在罚球线上投篮的结果,
投篮次数(n)
50
100
150
209
250
300
350
投中次数(m)
28
60
78
104
123
152
175
投中频率(n/m)
0.56
0.60
0.49
(1)计算并填写表中的投中频率(精确到0.01);
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?
相关试题

