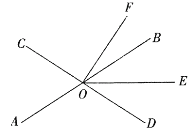
【题目】如图,直线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 平分
平分![]() .
.
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() 平分
平分![]() ,∠BOF=12°,若设∠BOE=x°.
,∠BOF=12°,若设∠BOE=x°.
①则![]() = . (用含
= . (用含![]() 的代数式表示)
的代数式表示)
②求![]() 的度数.
的度数.
参考答案:
【答案】(1)55°(2)①![]() ②104°
②104°
【解析】
(1)由对顶角的性质可知∠BOD=70°,从而可求得∠FOB=20°,由角平分线的定义可知∠BOE=![]() ∠BOD,最后根据∠EOF=∠BOE+∠FOB求解即可;
∠BOD,最后根据∠EOF=∠BOE+∠FOB求解即可;
(2)①先证明∠AOE=∠COE=x,然后由角平分线的定义可知∠FOE=![]() x;
x;
②∠BOE=∠FOE-∠FOB可知∠BOE=![]() x-15°,最后根据∠BOE+∠AOE=180°列出方程可求得x的值,从而可求得∠AOC的度数.
x-15°,最后根据∠BOE+∠AOE=180°列出方程可求得x的值,从而可求得∠AOC的度数.
(1)由对顶角相等可知:∠BOD=∠AOC=70°,
∵∠FOB=∠DOF-∠BOD,
∴∠FOB=90°-70°=20°,
∵OE平分∠BOD,
∴∠BOE=![]() ∠BOD=
∠BOD=![]() ×70°=35°,
×70°=35°,
∴∠EOF=∠FOB+∠BOE=35°+20°=55°,
(2)①∵OE平分∠BOD,∠BOE=x°,
∴∠DOE=∠BOE=x,
∵∠COE+∠DOE=180o,
∴∠COE=180o-xo,
∵OF平分∠COE,
∴∠FOE=![]() ∠COE=
∠COE=![]() ,
,
故答案为:![]() ;
;
②∵∠BOE=∠FOE-∠FOB,
∴∠BOE=![]() x-12°,
x-12°,
∵∠BOE+∠AOE=180°,
∴![]() x-12°+x=180°,
x-12°+x=180°,
解得:x=128°,
∴∠AOC=2∠BOE=2×(180°-128°)=104°.
-
科目: 来源: 题型:
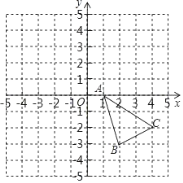
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(1,0),B(2,﹣3),C(4,﹣2).
(1)①画出△ABC关于x轴的对称图形△A1B1C1;②画出△A1B1C1向左平移3个单位长度后得到的△A2B2C2;
(2)如果AC上有一点P(m,n)经过上述两次变换,那么对应A2C2上的点P2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,是轴对称图形的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线
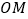 上有三点
上有三点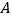 、
、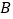 、
、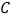 ,满足OA=30cm,AB=90cm,BC=15cm,点
,满足OA=30cm,AB=90cm,BC=15cm,点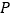 从点
从点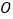 出发,沿
出发,沿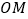 方向以
方向以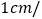 秒的速度匀速运动,点
秒的速度匀速运动,点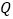 从点
从点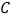 出发在线段
出发在线段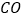 上向点
上向点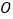 匀速运动,两点同时出发,当点
匀速运动,两点同时出发,当点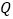 运动到点
运动到点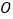 时,点
时,点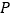 、
、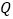 停止运动.
停止运动.(1)若点
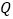 运动速度为
运动速度为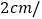 秒,经过多长时间
秒,经过多长时间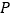 、
、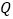 两点相遇?
两点相遇?(2)当
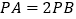 时,点
时,点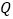 运动到的位置恰好是线段OB的中点,求点
运动到的位置恰好是线段OB的中点,求点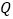 的运动速度;
的运动速度;(3)当点
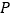 运动到线段
运动到线段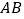 上时,分别取
上时,分别取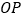 和
和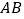 的中点
的中点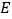 、
、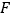 ,求
,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】六一期间,某公园游戏场举行“迎奥运”活动.有一种游戏的规则是:在一个装有6个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为40000人次,公园游戏场发放的福娃玩具为10000个.
(1)求参加一次这种游戏活动得到福娃玩具的概率;
(2)请你估计袋中白球接近多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各式分解因式:
(1)4x3-6x2;
(2)2a2b+5ab+b;
(3)6p(p+q)-4q(p+q);
(4)(x-1)2-x+1;
(5)-3a2b+6ab2-3ab.
相关试题

