【题目】如图,在△ABC中,∠C=90°,∠A=30°,CD=2cm, AB的垂直平分线MN交AC于D,连结BD,则AC的长是___________cm.

参考答案:
【答案】6
【解析】
由MN是AB的垂直平分线,即可得AD=BD,根据等腰三角形的性质,即可求得∠DBA的度数,又由直角三角形的性质,求得∠CBD=∠ABD=30°,然后根据角平分线的性质,求得DN的值,继而求得AD的值,则可求得答案.
∵MN是AB的垂直平分线,
∴AD=BD,DN⊥AB,
∴∠DBA=∠A=30°,
∵∠C=90°,
∴∠ABC=90°-∠A=60°,
∴∠CBD=∠ABD=30°,
∴DN=CD=2cm,
∴AD=2DN=4cm,
∴AC=AD+CD=6(cm).
故答案为:6.
-
科目: 来源: 题型:
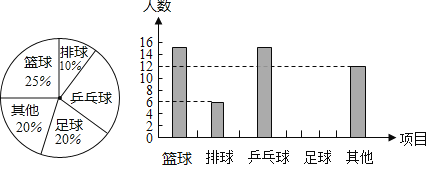
查看答案和解析>>【题目】某课外研究小组为了解学生参加课外体育活动的情况,采取抽样调查的方法从篮球、排球、乒乓球、足球及其他等五个方面调查了若干名同学的兴趣爱好(每人只能选其中一项),并将调查结果绘制成统计图,请根据图中提供的信息解答下列问题:
(1)在这次考察中一共调查了 名学生,请补全条形统计图;
(2)被调查同学中恰好有5名学来自初一12班,其中有2名同学选择了篮球,有3名同学选择了乒乓球,曹老师打算从这5名同学中选择两同学了解他们对体育社团的看法,请用列表法或画树状图法,求选出的两人恰好为一人选择篮球、一人选择乒乓球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程.
(1)(2x+3)2-16=0;
(2)(x-2)2-3x(x-2)=0.
(3)x2+4x=2
(4)x(x+4)=8x+12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,坡AB的坡比为1:2.4,坡长AB=130米,坡AB的高为BT.在坡AB的正面有一栋建筑物CH,点H、A、T在同一条地平线MN上.

(1)试问坡AB的高BT为多少米?
(2)若某人在坡AB的坡脚A处和中点D处,观测到建筑物顶部C处的仰角分别为60°和30°,试求建筑物的高度CH.(精确到米,
 ≈1.73,
≈1.73,  ≈1.41)
≈1.41) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

-
科目: 来源: 题型:
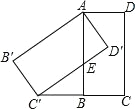
查看答案和解析>>【题目】如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点 C的对应点 C′恰好落在CB的延长线上,边AB交边 C′D′于点E.
(1)求证:BC=BC′;
(2)若 AB=2,BC=1,求AE的长.
-
科目: 来源: 题型:
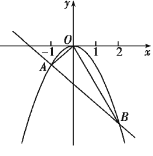
查看答案和解析>>【题目】已知二次函数y=ax2(a≠0)与一次函数y=kx-2的图象相交于A.B两点,如图所示,其中A(-1,-1).
(1)求二次函数和一次函数的解析式;
(2)求△OAB的面积.
相关试题

