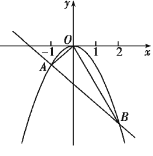
【题目】已知二次函数y=ax2(a≠0)与一次函数y=kx-2的图象相交于A.B两点,如图所示,其中A(-1,-1).
(1)求二次函数和一次函数的解析式;
(2)求△OAB的面积.
参考答案:
【答案】(1)y=-x2;(2)3
【解析】
(1)利用点A的坐标可求出直线与抛物线的解析式;
(2)求出点G的坐标及点B的坐标,利用S△OAB=![]() OG|A的横坐标|+
OG|A的横坐标|+![]() OG点B的横坐标求解即可.
OG点B的横坐标求解即可.
(1)∵一次函数y=kx-2的图象过点A(-1,-1),
∴-1=-k-2,解得k=-1,
∴一次函数的解析式为y=-x-2.
∵y=ax2过点A(-1,-1),
∴-1=a×(-1)2,解得a=-1,
∴二次函数的解析式为y=-x2.
(2)设AB交y轴于点G,过B作BH⊥OG于点H.
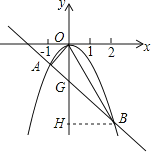
在y=-x-2中,令x=0,得y=-2,
∴G(0,-2),
联立一次函数与二次函数解析式可得![]()
解得![]() 或
或![]()
∴B(2,-4),∴BH=2.
∴S△OAB=S△AOG+S△BOG=![]() ×2×1+
×2×1+![]() ×2×2=1+2=3.
×2×2=1+2=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠A=30°,CD=2cm, AB的垂直平分线MN交AC于D,连结BD,则AC的长是___________cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

-
科目: 来源: 题型:
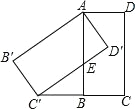
查看答案和解析>>【题目】如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点 C的对应点 C′恰好落在CB的延长线上,边AB交边 C′D′于点E.
(1)求证:BC=BC′;
(2)若 AB=2,BC=1,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在方程ax=12(a是正整数)中,x是未知数,a是用字母表示的已知数。于是,在项ax中,字母a是_____________,我们把a叫做_____________。这个方程是含有系数的_____________。在方程
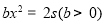 中,
中,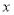 是未知数,b和s是用字母表示的已知数。同样地,字母b是______________字母s也叫做__________________,这个方程是含有系数的_____________。
是未知数,b和s是用字母表示的已知数。同样地,字母b是______________字母s也叫做__________________,这个方程是含有系数的_____________。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,
 ,
, 的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,
的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点, ,垂足为G,若
,垂足为G,若 ,则AE的边长为
,则AE的边长为


A.
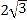 B.
B.  C. 4 D. 8
C. 4 D. 8 -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列关于x或y的方程。




相关试题

