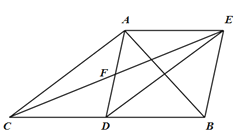
【题目】如图,在△ABC中,点D是BC的中点,点F是AD的中点,过点D作DE∥AC,交CF的延长线于点E,连接BE,AE.
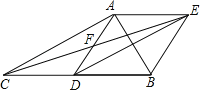
(1)求证:四边形ACDE是平行四边形;
(2)若AB=AC,试判断四边形ADBE的形状,并证明你的结论.
参考答案:
【答案】见试题解析
【解析】
试题分析:(1)首先证明△AFC≌△DFE,根据全等三角形对应边相等可得AC=DE,再根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)首先证明四边形ADBE为平行四边形,再根据等腰三角形的性质可得AD⊥CB,进而可得四边形ADBE为矩形.
试题解析:(1)证明:∵DE∥AC,
∴∠CAF=∠EDF,
∵点F是AD的中点,
∴FA=DF,
在△AFC和△DFE中

∴△AFC≌△DFE(ASA),
∴AC=DE,
∴四边形ACDE是平行四边形;
(2)解:四边形ADBE为矩形,理由如下:
∵四边形ACDE是平行四边形,
∴AE=CD且AE∥CB,
∵点D是BC的中点,
∴CD=DB,
∴AE=BD且AE∥DB,
∴四边形ADBE为平行四边形,
又∵AB=AC,
∴AD⊥CB,
∴∠ADB=90°,
∴四边形ADBE为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.根据两人的作法可判断( )

A. 甲正确,乙错误 B. 乙正确,甲错误
C. 甲、乙均正确 D. 甲、乙均错误
-
科目: 来源: 题型:
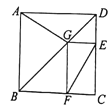
查看答案和解析>>【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为 m.
-
科目: 来源: 题型:
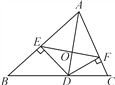
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠BAC=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.其中正确的是_________.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AFD=∠1,AC∥DE.
(1)试说明:DF∥BC;
(2)若∠1=68°,DF平分∠ADE,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,已知点O(0,0),A(1,0),B(1,1),C(2,0),△OBC的面积记为S1 , 过O、B、C三点的半圆面积记为S2;过O、B、C三点的抛物线与x轴所围成的图形面积记为S3 , 则S1、S2、S3的大小关系是 . (用“>”连接)
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:(1)如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数. 小颖同学的解题思路是:如图2,过点P作PE∥AB,请你接着完成解答.

问题迁移:
(2)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?

(提示:过点P作PE∥AD),请说明理由;
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你猜想∠CPD、∠α、∠β之间的数量关系.

相关试题

