搜索
【题目】将正方形ABCD绕点A按逆时针方向旋转30°，得正方形AB1C1D1 ， B1C1交CD于点E，AB= 
，则四边形AB1ED的内切圆半径为（ ） 
A.
B.
C.
D.
参考答案：
【答案】B
【解析】解：作∠DAF与∠AB1G的角平分线交于点O，过O作OF⊥AB1 ，
则∠OAF=30°，∠AB1O=45°，
故B1F=OF= 
OA，
设B1F=x，则AF= 
﹣x，
故（ ﹣x）2+x2=（2x）2 ，
解得x= 
或x= 
（舍去），
∴四边形AB1ED的内切圆半径为： ．
故选：B．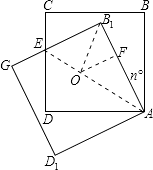
【考点精析】解答此题的关键在于理解正方形的性质的相关知识，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形，以及对三角形的内切圆与内心的理解，了解三角形的内切圆的圆心是三角形的三条内角平分线的交点，它叫做三角形的内心．
-
科目： 来源： 题型：
查看答案和解析>>【题目】标准的篮球场长28m，宽15m.在某场篮球比赛中，红队甲、乙两名运动员分别在A，B处，位置如图①所示，已知点B到中线EF的距离为6m，点C到中线EF的距离为8m，运动员甲在A处抢到篮球后，迅速将球抛向C处，球的平均运行速度是
m/s，运动员乙在B处看到后同时快跑到C处并恰好接住了球(点A，B，C在同一直线上)．图②中l1，l2分别表示球、运动员乙离A处的距离y(m)与从A处抛球后的时间x(s)的关系图象．(1)直接写出a，b，c的值；
(2)求运动员乙由B处跑向C处的过程中y(m)与x(s)的函数解析式l2；
(3)运动员要接住球，一般在球距离自己还有2m远时要做接球准备，求运动员乙准备接此球的时间．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，A，B两地相距450千米，两地之间有一个加油站O，且AO＝270千米，一辆轿车从A地出发，以每小时90千米的速度开往B地，一辆客车从B地出发，以每小时60千米的速度开往A地，两车同时出发，设出发时间为t小时．
（1）经过几小时两车相遇？
（2）当出发2小时时，轿车和客车分别距离加油站O多远？
（3）经过几小时，两车相距50千米？
-
科目： 来源： 题型：
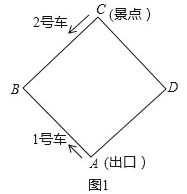
查看答案和解析>>【题目】如图，某景区内的环形路是边长为1200米的正方形ABCD，现有1号、2号两辆游览车分别从出口A和景点C同时出发，1号车沿A→B→C→D→A路线、2号车沿C→B→A→D→C路线连续循环行驶，供游客随时免费乘车（上、下车的时间忽略不计），两车速度均为300米/分．
（1）如图1，设行驶时间为t分（0≤t≤8）
①1号车、2号车离出口A的路程分别为_____米，_____米；（用含t的代数式表示）
②当两车相距的路程是600米时，求t的值；
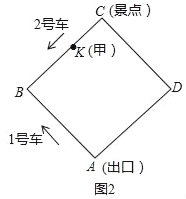
（2）如图2，游客甲在BC上的一点K（不与点B、C重合）处候车，准备乘车到出口A，设CK=x米．
情况一：若他刚好错过2号车，则他等候并搭乘即将到来的1号车；
情况二：若他刚好错过1号车，则他等候并搭乘即将到来的2号车．
请判断游客甲在哪种情况下乘车到出口A用时较多？（含候车时间）
-
科目： 来源： 题型：
查看答案和解析>>【题目】设二次函数y1=a（x﹣x1）（x﹣x2）（a≠0，x1≠x2）的图象与一次函数y2=dx+e（d≠0）的图象交于点（x1 ， 0），若函数y=y1+y2的图象与x轴仅有一个交点，则（ ）
A.a（x1﹣x2）=d
B.a（x2﹣x1）=d
C.a（x1﹣x2）2=d
D.a（x1+x2）2=d -
科目： 来源： 题型：
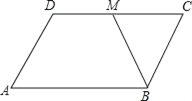
查看答案和解析>>【题目】如图，在平行四边形ABCD中，BM是∠ABC的平分线，交CD于点M，且DM＝2，平行四边形ABCD的周长是14，则BC的长等于（ ）
A. 2B. 2.5C. 3D. 3.5
-
科目： 来源： 题型：
查看答案和解析>>【题目】在数轴上，点A，O，B分别表示﹣15，0，9，点P，Q分别从点A，B同时开始沿数轴正方向运动，点P的速度是每秒3个单位，点Q的速度是每秒1个单位，运动时间为t秒．在运动过程中，若点P，Q，O三点其中一个点恰好是另外两点为端点的线段的一个三等分点，则运动时间为_____秒．
相关试题
