【题目】如图,在Rt△ABC中,∠A=30°,∠C=90°,E是斜边AB的中点,点P为AC边上一动点,若Rt△ABC的直角边AC=4,则PB+PE的最小值等于_____.

参考答案:
【答案】4
【解析】
如图所示,作点B关于AC的对称点D,连接PD,则可得PB+PE=PD+PE,当E,P,D在同一直线上时,PB+PE的最小值即为线段DE的长,据此求解即可得.
如图所示,作点B关于AC的对称点D,连接PD,则PB=PD,
∴PB+PE=PD+PE,
当E,P,D在同一直线上时,PB+PE的最小值即为线段DE的长,
∵Rt△ABC中,∠A=30°,∠C=90°,E是斜边AB的中点,
∴AB=2BE=2BC=BD,∠ABC=∠DBE,
∴△ABC≌△DBE,
∴DE=AC=4,
∴PB+PE的最小值等于4,
故答案为:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在△ABC中,AD是BC边的中线,过A点作AE∥BC与过D点作DE∥AB交于点E,连接CE.

(1)求证:四边形ADCE是平行四边形.
(2)连接BE,AC分别与BE、DE交于点F、G,如图(2),若AC=6,求FG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将两块相同的三角板(含30°角)按图中所示位置摆放,若BE交CF于D,AC交BE于M,AB交CF于N,则下列结论中错误的是( )
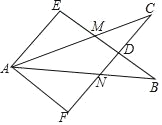
A. ∠EAC=∠FAB B. ∠EAF=∠EDF C. △ACN≌△ABM D. AM=AN
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价) 甲
乙
进价(元/件)
20
30
售价(元/件)
29
40
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县在实施“村村通”工程中,决定在A、B两村之间修一条公路,甲、乙两个工程队分别从A、B两村同时开始相向修路,施工期间,甲队改变了一次修路速度,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到公路修通,甲、乙两个工程队各自所修公路的长度y(米)与修路时间x(天)之间的函数图象如图所示.

(1)求甲队前8天所修公路的长度;
(2)求甲工程队改变修路速度后y与x之间的函数关系式;
(3)求这条公路的总长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC中,AB=AC,点P为边BC上异于B和C的任意一点,过点P作PD⊥AB于D,作PE⊥AC于E,过点C作CF⊥AB于F,求证:PD+PE=CF.

(1)有下面两种证明思路:(一)如图②,连接AP,由△ABP于△ACP面积之和等于△ABC的面积证得PD+PE=CF.(二)如图②,过点P作PG⊥CF,垂足为G,可以证明:PD=GF,PE=CG,则PD+PE=CF.
请你选择其中的一种证明思路完成证明:
(2)探究:如图③,当点P在BC的延长线上时,其它条件不变,探究并证明PD、PE和CF间的数量关系;
(3)猜想:当点P在CB的延长线上时,其它条件不变,猜想PD、PE和CF间的数量关系(不要求证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点A,O,B对应的数分别为﹣5,0,1,点M为数轴上任意一点,其对应的数为x.
请回答问题:

(1)A、B两点间的距离是_____,若点M到点A、点B的距离相等,那么x的值是_____;
(2)若点A先沿着数轴向右移动6个单位长度,再向左移动4个单位长度后所对应的数字是 ____ ;
(3)当x为何值时,点M到点A、点B的距离之和是8;
(4)如果点M以每秒3个单位长度的速度从点O向左运动时,点A和点B分别以每秒1个单位长度和每秒4个单位长度的速度也向左运动,且三点同时出发,那么几秒种后点M运动到点A、点B之间,且点M到点A、点B的距离相等?
相关试题

