【题目】已知,如图,抛物线![]() 与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在![]() 轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)抛物线的解析式![]()
(2)四边形ABCD面积有最大值为![]() ;
;
(3)存在3个点符合题意,坐标分别是P1(-2,-3), ![]() ,
, ![]()
【解析】试题分析:(1)、根据题意得出点B和点C的坐标,然后代入函数解析式求出答案;(2)、首先根据点A和点C的坐标得出直线AC的解析式,然后过点D作DM∥y轴分别交线段AC和x轴于点M,N,设点M的坐标为(m,-m-3),从而得出点D的坐标,求出DM的长度,根据二次函数的性质求出DM的最大值,得出面积的最大值;(3)、①、过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,,将C(0,-3)代入函数解析式求出点P的坐标;②、平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,设出点P的坐标为(x,3),然后代入函数解析式求出点P的坐标.
试题解析:(1)、∵OC=3OB,B(1,0),∴C(0,-3). 把点B,C的坐标代入![]() ,得
,得![]()
∴抛物线的解析式![]()
(2)、由A(-3,0),C(0,-3)得直线AC的解析式为![]() ,
,
如图,过点D作DM∥y轴分别交线段AC和x轴于点M,N.
设M![]() 则D
则D![]() ,
, ![]()
∴-1<0,∴当x=![]() 时,DM有最大值
时,DM有最大值![]() ∴S四边形ABCD=S△ABC+S△ACD
∴S四边形ABCD=S△ABC+S△ACD![]()
此时四边形ABCD面积有最大值为![]() .
.
(3)、存在
①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,
此时四边形ACP1E1为平行四边形. ∵C(0,-3),令![]()
∴![]() ,
, ![]() .∴P1(-2,-3).
.∴P1(-2,-3).
②平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,∵C(0,-3),
∴可令P(x,3), ![]() ,得
,得![]() 解得
解得![]() ,
, ![]()
此时存在点![]() ,
,![]()
综上所述,存在3个点符合题意,坐标分别是P1(-2,-3), ![]()
![]()


-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:-22+3÷(-1)2013-∣-4∣×5
-
科目: 来源: 题型:
查看答案和解析>>【题目】[6a2b2+___+____]÷2ab2=3a+b-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:(a-2)2-(a-1)·(a+1)+5a,其中a=-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一名射击爱好者5次射击的中靶环数如下:6,7,9,8,9,这5个数据的中位数是( )
A.6
B.7
C.8
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和
矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的
距离是11m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线的解析式;
(2)已知从某时刻开始的40h内,水面与河底ED的距离h(单位:m)随时间t(单位:h)的变化满足函数
关系
 且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于
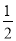 MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )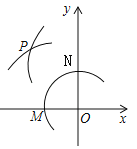
A. a=b B. 2a﹣b=1 C. 2a+b=﹣1 D. 2a+b=1
相关试题

