【题目】如图,已知抛物线y=![]()
![]() ﹣
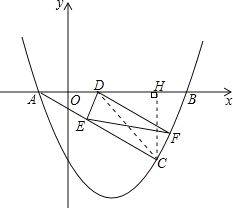
﹣![]() x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.

(1)、求点A和点B的坐标;
(2)、求证:四边形DECF是矩形;
(3)、连接EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.
参考答案:
【答案】(1)、(﹣1,0),(4,0);(2)、证明过程见解析;(3)、2.
【解析】
试题分析:(1)、根据抛物线的解析式来求点A、B的坐标即可;(2)、欲证明四边形DECF是矩形,只需证得四边形DECF是平行四边形且有一内角为直角即可;(3)、连接CD,根据矩形DECF的对角线相等得到:EF=CD.当CD⊥AB时,CD的值最小,即EF的值最小.
试题解析:(1)、当y=0时,![]()
![]() ﹣
﹣![]() x﹣2=0, 解方程,得 x1=﹣1,x2=4. ∵点A在点B的左侧,
x﹣2=0, 解方程,得 x1=﹣1,x2=4. ∵点A在点B的左侧,
∴点A、B的坐标分别是(﹣1,0),(4,0);
(2)、把C(m,1﹣m)代入y=![]()
![]() ﹣
﹣![]() x﹣2得:
x﹣2得:![]() -2=1-m 解方程,得m=3或m=﹣2.
-2=1-m 解方程,得m=3或m=﹣2.
∵点C位于第四象限, ∴m>0,1﹣m<0,即m>1, ∴m=﹣2舍去, ∴m=3,
∴点C的坐标为(3,﹣2). 过点C作CH⊥AB于H,则∠AHC=∠BHC=90°.
由A(﹣1,0),B(4,0),C(3,﹣2)得到:AH=4,CH=2,BH=1,AB=5, ∴![]() =2.
=2.
又∵∠AHC=∠CHB=90°,∴△AHC∽△CHB, ∴∠ACH=∠CBH. ∵∠CBH+∠BCH=90°,
∴∠ACH+∠BCH=90°, ∴∠ACB=90°, ∵DE∥BC,DF∥AC, ∴四边形DECF是平行四边形,
∴平行四边形DECF是矩形;
(3)、存在.理由如下: 连接CD. ∵平行四边形DECF是矩形, ∴EF=CD.
当CD⊥AB时,CD的值最小. ∵C(3,2), ∴DC的最小值是2, ∴EF的最小值是2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2b﹣6ab2+9b3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是( )
A. 有理数是有限小数 B. 有理数是有限小数
C. 有理数是无限循环小数 D. 无限不循环小数是无理数
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2y﹣4y结果正确的是( )
A.y(x2﹣4)
B.y(x﹣2)2
C.y(x+2)2
D.y(x+2)(x﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】作图题
如图,在6×6的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形.
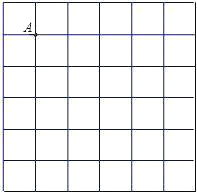
(1)从点A出发的一条线段AB,使它的另一个端点落在格点(即小正方形的顶点)上,且长度为
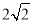 ;
;(2)以(1)中的AB为边的一个等腰三角形ABC,使点C在格点上,且另两边的长都是无理数;
(3)画出△ABC关于点B的中心对称图形△A1B1C1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米.
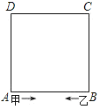
(1)出发后 分钟时,甲乙两人第一次在正方形的顶点处相遇;
(2)如果用记号(a,b)表示两人行了a分钟,并相遇过b次,那么当两人出发后第一次处在正方形的两个相对顶点位置时,对应的记号应是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数的绝对值等于它的相反数,那么这个数是( )
A.是正数
B.是负数
C.是非负数
D.是非正数
相关试题

