【题目】如图顺次连接等腰梯形四边中点得到一个四边形,再顺次连接所得四边形四边的中点得到的图形是( )
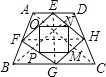
A. 等腰梯形B. 直角梯形C. 菱形D. 矩形
参考答案:
【答案】D
【解析】
首先作出图形,根据三角形的中位线定理,可以得到![]() ,
,![]() ,
,![]() ,
,![]() 再根据等腰梯形的对角线相等,即可证得四边形EFGH的四边相等,即可证得是菱形,然后根据三角形中位线定理即可证得四边形OPMN的一组对边平行且相等,则是平行四边形,在根据菱形的对角线互相垂直,即可证得平行四边形的一组临边互相垂直,即可证得四边形OPMN是矩形.
再根据等腰梯形的对角线相等,即可证得四边形EFGH的四边相等,即可证得是菱形,然后根据三角形中位线定理即可证得四边形OPMN的一组对边平行且相等,则是平行四边形,在根据菱形的对角线互相垂直,即可证得平行四边形的一组临边互相垂直,即可证得四边形OPMN是矩形.
解:连接AC,BD.
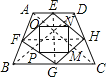
∵E,F是AB,AD的中点,即EF是![]() 的中位线.
的中位线.
![]() ,
,
同理:![]() ,
,![]() ,
,![]() .
.
又![]() 等腰梯形ABCD中,
等腰梯形ABCD中,![]() .
.
![]() .
.
![]() 四边形EFGH是菱形.
四边形EFGH是菱形.
![]() 是
是![]() 的中位线,
的中位线,
∴EF![]() EG,
EG,![]() ,
,
同理,NM![]() EG,
EG,
∴EF![]() NM,
NM,
![]() 四边形OPMN是平行四边形.
四边形OPMN是平行四边形.
![]() ,
,![]() ,
,
又![]() 菱形EFGH中,
菱形EFGH中,![]() ,
,![]()
![]() 平行四边形OPMN是矩形.
平行四边形OPMN是矩形.
故选:D.
-
科目: 来源: 题型:
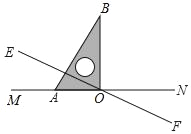
查看答案和解析>>【题目】如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与点O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒5°的速度沿顺时针方向旋转一周,设运动时间为t(s).
(1)当t为何值时,直角边OB恰好平分∠NOE?此时OA是否平分∠MOE?请说明理由;
(2)若在三角尺转动的同时,直线EF也绕点O以每秒8°的速度顺时针方向旋转一周,当一方先完成旋转一周时,另一方同时停止转动.
①当t为何值时,OE平分∠AOB?
②OE能否平分∠NOB?若能请直接写出t的值;若不能,请说明理由.
-
科目: 来源: 题型:
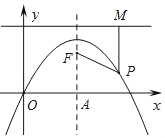
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2x的对称轴与x轴交于点A,点F在抛物线的对称轴上,且点F的纵坐标为
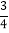 .过抛物线上一点P(m,n)向直线y=
.过抛物线上一点P(m,n)向直线y=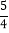 作垂线,垂足为M,连结PF.
作垂线,垂足为M,连结PF.(1)当m=2时,求证:PF=PM;
(2)当点P为抛物线上任意一点时,PF=PM是否还成立?若成立,请给出证明;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AC⊥BC于C,BC=a,CA=b,AB=c,下列图形中⊙O与△ABC的某两条边或三边所在的直线相切,则⊙O的半径为
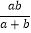 的是( )
的是( )A.
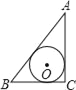 B.
B. 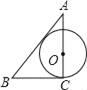 C.
C. 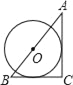 D.
D. 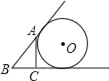
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2
 cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:(1)正整数和负整数统称为整数;(2)把能够写成分数形式
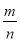 (m、n是整数,n≠0)的数叫做有理数;(3)异号两数相加,当绝对值不等时,取绝对值较大加数的符号,并用较大的加数减去较小的加数;(4)0是整数,但不是整式.正确的个数有 ( )
(m、n是整数,n≠0)的数叫做有理数;(3)异号两数相加,当绝对值不等时,取绝对值较大加数的符号,并用较大的加数减去较小的加数;(4)0是整数,但不是整式.正确的个数有 ( )A.0个B.1个C.2个D.3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】用同样大小的两种不同颜色的正方形纸片,按图的方式拼正方形.

(1)第①个图形中有1个小正方形,第②个图形中有4个小正方形,第③个图形中有9个小正方形,第⑦个图形中有__________个小正方形.
(2)第⑩个图形比第⑨个图形多_________个小正方形.
(3)第n个图形比第n-1个图形多_________个小正方形.
相关试题

