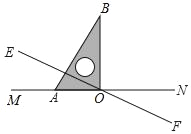
【题目】如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与点O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒5°的速度沿顺时针方向旋转一周,设运动时间为t(s).
(1)当t为何值时,直角边OB恰好平分∠NOE?此时OA是否平分∠MOE?请说明理由;
(2)若在三角尺转动的同时,直线EF也绕点O以每秒8°的速度顺时针方向旋转一周,当一方先完成旋转一周时,另一方同时停止转动.
①当t为何值时,OE平分∠AOB?
②OE能否平分∠NOB?若能请直接写出t的值;若不能,请说明理由.
参考答案:
【答案】(1)t=3,此时OA平分∠MOE;(2)①t=5;②t=![]() .
.
【解析】
(1)根据:角度=速度×时间进行计算,由等量关系:直角边OB恰好平分∠NOE,列出方程求解即可.
(2)①用t表示∠AOE的度数令其等于45°即可求;
②用t表示∠NOE、∠BOE的度数然后列方程解决.
(1)∵当直角边OB恰好平分∠NOE时,∠NOB= ![]() ∠NOE=
∠NOE= ![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∴90﹣5t=75,
解得:t=3,
此时∠MOA=5°×3=15°= ![]() ∠MOE,
∠MOE,
∴此时OA平分∠MOE.
(2)①若OE平分∠AOB,
由题意得 30+8t﹣5t=90÷2,
解得 t=5;
②若OE平分∠NOB上面,
由题意得180﹣(30°+8t)= ![]() (90﹣5t),
(90﹣5t),
解得t=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C、D是线段AB上两点,已知AC:CD:DB=1:2:3,M、N分别为AC、DB的中点,且AB=12cm,
(1)求线段CD的长;
(2)求线段MN的长.
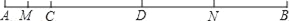
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=40°,求∠DOE的度数;
(2)如图①,若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示)
(3)将图①中的∠COD绕顶点O顺时针旋转至图②的位置,OE平分∠BOC.
①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
②在∠AOC的内部有一条射线OF,且∠AOC﹣3∠AOF=2∠BOE,试确定∠AOF与∠DOE的度数之间的关系,说明理由.
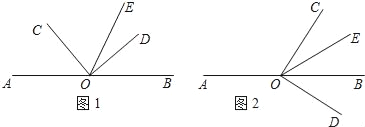
-
科目: 来源: 题型:
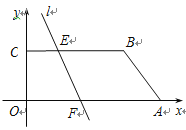
查看答案和解析>>【题目】如图,在直角坐标系中,O(0,0),A(7,0),B(5,2),C(0,2)一条动直线l分别与BC、OA交于 点E、F,且将四边形OABC分为面积相等的两部分,则点C到动直线l的距离的最大值为____,
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
消费卡
消费方式
普通卡
35元/次
白金卡
280元/张,凭卡免费消费10次再送2次
钻石卡
560元/张,凭卡每次消费不再收费
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用
(Ⅰ)若每年去该健身中心6次,应选择哪种消费方式更合算?
(Ⅱ)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(Ⅲ)若某位顾客每年去该健身中心健身至少18次,请通过计算帮助这位顾客选择最合算的消费方式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠B、∠C的平分线交于P,且分别与AD交于E、F,
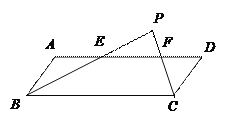
(1)求证:△BPC为直角三角形;
(2)若BC=16,CD=3,PE=8,求△PEF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】制造厂的某车间生产圆形铁片和长方形铁片,如图,两个圆形铁片和一个长方形铁片可以制造成一个油桶.已知该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或者长方形铁片80片.问安排生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?

相关试题

