【题目】如图所示是甲乙两个工程队完成某项工程的进度图,首先是甲独做了10天,然后两队合做,完成剩下的工程.

(1)甲队单独完成这项工程,需要多少天?
(2)求乙队单独完成这项工程需要的天数;
(3)实际完成的时间比甲独做所需的时间提前多少天?
参考答案:
【答案】(1)40天;(2)60天;(3)12天 .
【解析】
(1)由第一段图像可知,甲队独做10天完成总工作量的0.25,则可求出甲的工作效率,再用总量1除以这个效率即可得出甲队单独完成这项工程需要的天数;
(2)由第二段图像可知,甲乙6天完成总量的(0.5-0.25)即0.25,甲6天做的工作量可求,于是求出乙6天的工作量,进而求出乙的工作效率,再用总量除以这个效率即可得出乙队单独完成这项工程需要的天数;
(3)因为甲队独做用40天,再求出实际完成的时间,两个数相减即可,甲乙合作完成了总量的0.75,除以他们的效率和再加上10,即是实际完成的时间,用40减这个数值即可得出结论.
(1)因为甲队独做10天完成总工作量的0.25,
所以甲一天做了0.25÷10=![]() ,
,
于是甲队单独完成这项工程需要的天数为:1÷![]() =40天;
=40天;
(2)甲乙6天完成总量的(0.5-0.25)即0.25,
则乙6天的工作量是0.25-![]() ×6=
×6=![]() ,
,
所以乙的效率是![]() ÷6=
÷6=![]() ,
,
所以乙队单独完成这项工程需要的天数为1÷![]() =60天;
=60天;
(3)甲乙合作完成了总量的0.75,除以他们的效率和再加上10,即是实际完成的时间,
即0.75÷(![]() +
+![]() )+10=18+10=28(天),
)+10=18+10=28(天),
因为甲队独做需用40天,
所以40-28=12天,
故实际完成的时间比甲独做所需的时间提前12天.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小军和小明玩一种抽卡片游戏,他们拿了八张扑克牌,将数字为
 、
、 、
、 、
、 的四张牌给小军,将数字为
的四张牌给小军,将数字为 、
、 、
、 、
、 的四张牌给小明,并按如下游戏规则进行:小军和小明各自的四张牌中随机抽出一张,然后将抽出的两张牌数字相加,若和为偶数,小军赢,若和为奇数,则小明赢.
的四张牌给小明,并按如下游戏规则进行:小军和小明各自的四张牌中随机抽出一张,然后将抽出的两张牌数字相加,若和为偶数,小军赢,若和为奇数,则小明赢. 请用树状图或列表法求小军获胜的概率.
请用树状图或列表法求小军获胜的概率. 这个游戏公平吗?请说明理由.
这个游戏公平吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=90°,D为AC上一点,E为BC上一点,点A和点E关于BD对称,点B和点C关于DE对称.求∠ABC和∠C的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y1=2x-4与y2=-2x+8的图象,观察图象并回答问题:

(1)x取何值时,2x-4>0?
(2)x取何值时,-2x+8>0?
(3)x取何值时,2x-4>0与-2x+8>0同时成立?
(4)求函数y1=2x-4与y2=-2x+8的图象与x轴所围成的三角形的面积?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小明设计两个可以自由转动的转盘,甲转盘被等分成
 个扇形,乙转盘被等分成
个扇形,乙转盘被等分成 个扇形,每个扇形上都标有相应的数字.小亮和小颖利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于
个扇形,每个扇形上都标有相应的数字.小亮和小颖利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于 ,小颖获胜;指针所指区域内的数字之和等于
,小颖获胜;指针所指区域内的数字之和等于 ,为平局;指针所指区域内的数字之和大于
,为平局;指针所指区域内的数字之和大于 ,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.
,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.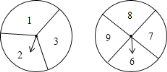
 转动转盘甲,转盘停止后,指针指向偶数的概率是________.
转动转盘甲,转盘停止后,指针指向偶数的概率是________. 在此游戏中,小颖获胜的概率是________.
在此游戏中,小颖获胜的概率是________. 你认为该游戏是否公平?若游戏规则公平,请说明理由;若游戏规则不公平,如果让你修改小明的方案,你认为应该从哪个方面入手(不用另外设计方案,只说明修改要点).
你认为该游戏是否公平?若游戏规则公平,请说明理由;若游戏规则不公平,如果让你修改小明的方案,你认为应该从哪个方面入手(不用另外设计方案,只说明修改要点). -
科目: 来源: 题型:
查看答案和解析>>【题目】建立模型:如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.

(1)操作:
过点A作AD⊥
 于点D,过点B作BE⊥
于点D,过点B作BE⊥ 于点E.求证:△CAD≌△BCE.
于点E.求证:△CAD≌△BCE.(2)模型应用:
①如图2,在直角坐标系中,直线
 :
: 与y轴交于点A,与x轴交于点B,将直线
与y轴交于点A,与x轴交于点B,将直线 绕着点A顺时针旋转45°得到直线
绕着点A顺时针旋转45°得到直线 .求直线
.求直线 的函数表达式.
的函数表达式.②如图3,在直角坐标系中,点B(4,3),作BA⊥y轴于点A,作BC⊥x轴于点C,P是直线BC上的一个动点,点Q(a,5a﹣2)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图案中,是轴对称图形的是( )
A.
 B.
B.
C.
 D.
D.
相关试题

