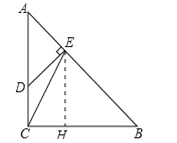
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,联结CE,求:
(1)线段BE的长;
(2)∠ECB的余切值.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由等腰直角三角形的性质得出∠A=∠B=45°,由勾股定理求出AB,求出∠ADE=∠A=45°,由三角函数得出AE,即可得出BE的长;
(2)过点E作EH⊥BC,垂足为点H,由三角函数求出EH=BH=BEcos45°=2,得出CH=1,在Rt△CHE中,由三角函数求出cot∠ECB=![]() =
=![]() 即可.
即可.
试题解析:(1)∵AD=2CD,AC=3,∴AD=2,∵在Rt△ABC中,∠ACB=90°,AC=BC=3,∴∠A=∠B=45°,AB=![]() =
=![]() =
=![]() ,∵DE⊥AB,∴∠AED=90°,∠ADE=∠A=45°,∴AE=ADcos45°=
,∵DE⊥AB,∴∠AED=90°,∠ADE=∠A=45°,∴AE=ADcos45°=![]() =
=![]() ,∴BE=AB﹣AE=
,∴BE=AB﹣AE=![]() =
=![]() ,即线段BE的长为
,即线段BE的长为![]() ;
;
(2)过点E作EH⊥BC,垂足为点H,如图所示:
∵在Rt△BEH中,∠EHB=90°,∠B=45°,∴EH=BH=BEcos45°=![]() =2,∵BC=3,∴CH=1,在Rt△CHE中,cot∠ECB=
=2,∵BC=3,∴CH=1,在Rt△CHE中,cot∠ECB=![]() =
=![]() ,即∠ECB的余切值为
,即∠ECB的余切值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索研究.请解决下列问题:
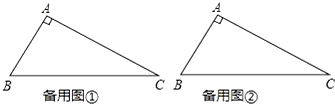
(1)已知△ABC中,∠A=90°,∠B=67.5°,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,并把所有不同的分割方法都画出来,图不够可以自己画.只需画图,不必说明理由,但要在图中标出相等两角的度数).
(2)已知等腰△ABC中,AB=AC,D为BC上一点,连接AD,若△ABD和△ACD都是等腰三角形,则∠B的度数为 (请画出示意图,并标明必要的角度).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某国发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作,如图,某探测对在地面A、B两处均探测出建筑物下方C处由生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米,参考数据:sin25°≈0.4,cos25°≈0,9,tan25°≈0.5,
 ≈1.7)
≈1.7)
-
科目: 来源: 题型:
查看答案和解析>>【题目】3x2可以表示为( )
A.x2+x2+x2
B.x2x2x2
C.3x3x
D.9x -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(2,﹣3)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】在“数学晚会”上,七年级的10个同学藏在10个大盾牌后面,男同学盾牌前面的结果是一
个正数,女同学盾牌前面的结果是一个负数,这10个盾牌如图所示,请你通过计算,求出盾牌后面男、女同学各有多少人.
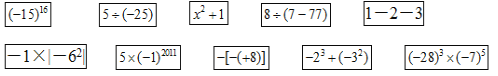
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A﹣C路径向终点C运动;点Q从B点出发沿B﹣C﹣A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.则点P运动时间为_________时,△PEC与△QFC全等.

相关试题

