【题目】我市新建火车站广场将投入使用,计划在广场内种植A,B两种花木共4000棵,若A花木数量是B花木数量的2倍还多400棵.
(1)求A,B两种花木的数量分别是多少棵?
(2)如果园林处安排24人同时种植这两种花木,每人每天能种植A花木70棵或B花木60棵,应怎样分别安排种植A花木和种植B花木的人数,才能确保同时完成各自的任务?
参考答案:
【答案】
(1)解:设A花木数量为x棵,则B花木数量是y棵,
依题意得: ![]() ,
,
解得 ![]() .
.
答:A花木数量为2800,则B花木数量是1200棵;
(2)解:设安排m人种植A花木,则安排(24﹣m)人种植B花木,
依题意得: ![]() =
= ![]() ,
,
解得m=16,经检验,m=16是原方程的解,且符合题意.
答:安排16人种植A花木,安排8人种植B花木
【解析】(1)首先设A花木数量为x棵,则B花木数量是y棵,由题意得等量关系:种植A,B两种花木共4000棵,A花木数量是B花木数量的2倍还多400棵,根据等量关系列出方程组,再解即可;(2)首先设安排m人种植A花木,由题意得等量关系:m人种植A花木所用时间=(24﹣m)人种植B花木所用时间,根据等量关系列出方程,再解即可.
【考点精析】解答此题的关键在于理解分式方程的应用的相关知识,掌握列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一根筷子一端放在水里,一端露出水面,筷子变弯了,它真的弯了吗?其实没有,这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变,图中与∠1是同位角的有____________,与∠2是内错角的有________________.
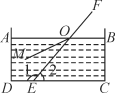
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,C是劣弧
 的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2.
的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2. 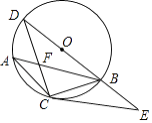
(1)求CB的长;
(2)延长DB到E,使BE=OB,连接CE,求证:CE是⊙O的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,(1)指出DC和AB被AC所截得的内错角;
(2)指出AD和BC被AE所截得的同位角;
(3)指出∠4与∠7,∠2与∠6,∠ADC与∠DAB各是什么关系的角,并指出各是哪两条直线被哪一条直线所截形成的.
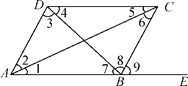
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:我们都知道,
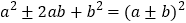
于是,-2x2+40x+5
=-2(x2-20x)+5
=-2(x2-20x+100)+200+5
=-2(x-10)2+205
又因为
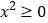 ,所以
,所以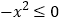 ,
,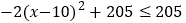
所以,-2x2+40x+5有最大值205.
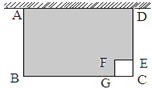
如图,某农户准备用长34米的铁栅栏围成一边靠墙的长方形羊圈ABCD和一个边长为1米的正方形狗屋CEFG.设AB=x米.
(1)请用含x的代数式表示BC的长(直接写答案);
(2)设山羊活动范围即图中阴影部分的面积为S,试用含x的代数式表示S,并计算当x=5时S的值;
(3)试求出山羊活动范围面积S的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,E为AD的中点,F为BC边上一动点,设BF=t(0≤t≤2),线段EF的垂直平分线GH分别交边CD,AB于点G,H,过E做EM⊥BC于点M,过G作GN⊥AB于点N.
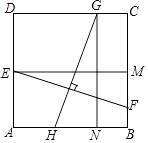
(1)当t≠2时,求证:△EMF≌△GNH;
(2)顺次连接E、H、F、G,设四边形EHFG的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过原点的直线y=k1x和y=k2x与反比例函数y=
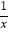 的图象分别交于两点A,C和B,D,连接AB,BC,CD,DA.
的图象分别交于两点A,C和B,D,连接AB,BC,CD,DA.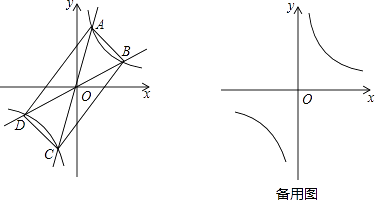
(1)四边形ABCD一定是四边形;(直接填写结果)
(2)四边形ABCD可能是矩形吗?若可能,试求此时k1 , k2之间的关系式;若不能,说明理由;
(3)设P(x1 , y1),Q(x2 , y2)(x2>x1>0)是函数y=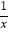 图象上的任意两点,a=
图象上的任意两点,a= 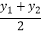 ,b=
,b= 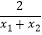 ,试判断a,b的大小关系,并说明理由.
,试判断a,b的大小关系,并说明理由.
相关试题

