【题目】如图,过原点的直线y=k1x和y=k2x与反比例函数y= ![]() 的图象分别交于两点A,C和B,D,连接AB,BC,CD,DA.
的图象分别交于两点A,C和B,D,连接AB,BC,CD,DA.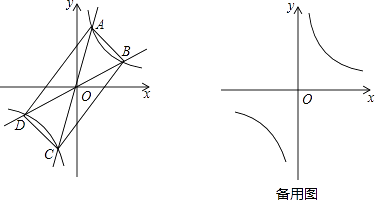
(1)四边形ABCD一定是四边形;(直接填写结果)
(2)四边形ABCD可能是矩形吗?若可能,试求此时k1 , k2之间的关系式;若不能,说明理由;
(3)设P(x1 , y1),Q(x2 , y2)(x2>x1>0)是函数y= ![]() 图象上的任意两点,a=
图象上的任意两点,a= ![]() ,b=
,b= ![]() ,试判断a,b的大小关系,并说明理由.
,试判断a,b的大小关系,并说明理由.
参考答案:
【答案】
(1)平行
(2)
解:∵正比例函数y=k1x(k1>0)与反比例函数y= ![]() 的图象在第一象限相交于A,
的图象在第一象限相交于A,
∴k1x= ![]() ,解得x=
,解得x= ![]() (因为交于第一象限,所以负根舍去,只保留正根)
(因为交于第一象限,所以负根舍去,只保留正根)
将x= ![]() 带入y=k1x得y=
带入y=k1x得y= ![]() ,
,
故A点的坐标为( ![]() ,
, ![]() )同理则B点坐标为(
)同理则B点坐标为( ![]() ,
, ![]() ),
),
又∵OA=OB,
∴ ![]() =
= ![]() ,两边平方得:
,两边平方得: ![]() +k1=
+k1= ![]() +k2,
+k2,
整理后得(k1﹣k2)(k1k2﹣1)=0,
∵k1≠k2,
所以k1k2﹣1=0,即k1k2=1;
(3)
解:∵P(x1,y1),Q(x2,y2)(x2>x1>0)是函数y= ![]() 图象上的任意两点,
图象上的任意两点,
∴y1= ![]() ,y2=
,y2= ![]() ,
,
∴a= ![]() =
= ![]() =
= ![]() ,
,
∴a﹣b= ![]() ﹣
﹣ ![]() =
= ![]() =
= ![]() ,
,
∵x2>x1>0,
∴ ![]() >0,x1x2>0,(x1+x2)>0,
>0,x1x2>0,(x1+x2)>0,
∴ ![]() >0,
>0,
∴a﹣b>0,
∴a>b.
【解析】解:(1)∵直线y=k1x和y=k2x与反比例函数y= ![]() 的图象关于原点对称,
的图象关于原点对称,
∴OA=OC,OB=OD,
∴四边形ABCD 是平行四边形;
所以答案是:平行;
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市新建火车站广场将投入使用,计划在广场内种植A,B两种花木共4000棵,若A花木数量是B花木数量的2倍还多400棵.
(1)求A,B两种花木的数量分别是多少棵?
(2)如果园林处安排24人同时种植这两种花木,每人每天能种植A花木70棵或B花木60棵,应怎样分别安排种植A花木和种植B花木的人数,才能确保同时完成各自的任务? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:我们都知道,
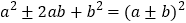
于是,-2x2+40x+5
=-2(x2-20x)+5
=-2(x2-20x+100)+200+5
=-2(x-10)2+205
又因为
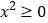 ,所以
,所以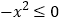 ,
,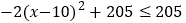
所以,-2x2+40x+5有最大值205.
如图,某农户准备用长34米的铁栅栏围成一边靠墙的长方形羊圈ABCD和一个边长为1米的正方形狗屋CEFG.设AB=x米.
(1)请用含x的代数式表示BC的长(直接写答案);
(2)设山羊活动范围即图中阴影部分的面积为S,试用含x的代数式表示S,并计算当x=5时S的值;
(3)试求出山羊活动范围面积S的最大值.
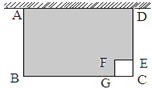
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,E为AD的中点,F为BC边上一动点,设BF=t(0≤t≤2),线段EF的垂直平分线GH分别交边CD,AB于点G,H,过E做EM⊥BC于点M,过G作GN⊥AB于点N.
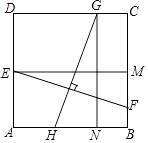
(1)当t≠2时,求证:△EMF≌△GNH;
(2)顺次连接E、H、F、G,设四边形EHFG的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,(1)∠2与∠B是什么角?若∠1=∠B,则∠2与∠B有何数量关系?请说明理由.
(2)∠3与∠C是什么角?若∠4+∠C=180°,则∠3与∠C有何数量关系?请说明理由.
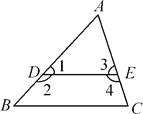
-
科目: 来源: 题型:
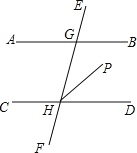
查看答案和解析>>【题目】如图,直线AB,CD被直线EF所截,点G,H为它们的交点,∠AGE与它的同位角相等,HP平分∠GHD.∠AGH∶∠BGH=2∶7,试求∠CHG和∠PHD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列图形:

它们是按一定规律排列的,依照此规律,第5个图形中的五角星的个数为___,第n个图形中的五角星(n为正整数)个数为____(用含n的代数式表示).
相关试题

