【题目】若a、b、c为△ABC的三边。
(1)判断代数式a![]() 2abc
2abc![]() +b
+b![]() 的值与0的大小关系,并说明理由;
的值与0的大小关系,并说明理由;
(2)满足a![]() +b
+b![]() +c
+c![]() =ab+ac+bc,试判断△ABC的形状.
=ab+ac+bc,试判断△ABC的形状.
参考答案:
【答案】(1)a![]() 2abc
2abc![]() +b
+b![]() <0;(2)△ABC是等边三角形.
<0;(2)△ABC是等边三角形.
【解析】
(1)根据完全平方公式和平方差公式先将代数式进行变形,然后利用三角形三边关系即可判断.
(2)根据完全平方公式将题目所给的等式进行变形,然后利用非负性即可求出答案.
(1) a![]() 2abc
2abc![]() +b
+b![]() =(ab)
=(ab) ![]() c
c![]() =(ab+c)(abc)
=(ab+c)(abc)
∵a+c>b,a<b+c,
∴ab+c>0,abc<0,
∴a![]() 2abc
2abc![]() +b
+b![]() <0
<0
(2)∵a![]() +b
+b![]() +c
+c![]() =ab+ac+bc
=ab+ac+bc
∴2a![]() +2b
+2b![]() +2c
+2c![]() 2ab2ac2bc=0,
2ab2ac2bc=0,
∴a![]() 2ab+b
2ab+b![]() +b
+b![]() 2bc+c
2bc+c![]() +a
+a![]() 2ac+c
2ac+c![]() =0,
=0,
∴(ab) ![]() +(bc)
+(bc) ![]() +(ac)
+(ac) ![]() =0,
=0,
∴ab=0,bc=0,ac=0,
∴a=b=c,
∴△ABC是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开设了丰富多彩的实践类拓展课程,分别设置了体育类、艺术类、文学类及其它类课程(要求人人参与,每人只能选择一门课程).为了解学生喜爱的拓展课类别,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:

(1)此次共调查了多少人?
(2)请将条形统计图补充完整
(3)求文学类课程在扇形统计图中所占圆心角的度数;
(4)若该校有1500名学生,请估计喜欢体育类拓展课的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1的解析式为y=﹣x+2,l1与x轴交于点B,直线l2经过点D(0,5),与直线l1交于点C(﹣1,m),且与x轴交于点A,
(1)求点C的坐标及直线l2的解析式;
(2)求△ABC的面积.

-
科目: 来源: 题型:
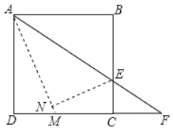
查看答案和解析>>【题目】如图,正方形ABCD的边长为8,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,当AB=2CF时,则NM的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市物价部门核定的市区出租车服务收费标准是:起步价5元(含2千米),以后每千米收费1元,超过10千米部分加收空驶费0.5元/公里,乘车前可免费等候5分钟,超时或途中等候加收1元/5分钟。
小林乘出租车从家去相距5千米的图书馆借书。他的行程情况如下图:
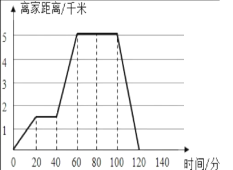
(1) 他去时需付车费多少元?
(2)返回时的速度是每小时行多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD是由六个正方形组成的完美长方形,中间最小正方形的面积是1,最大正方形的边长为x.

(1)用x的代数式表示长方形ABCD的长是______或______、宽是______;
(2)求长方形ABCD的面积.
-
科目: 来源: 题型:
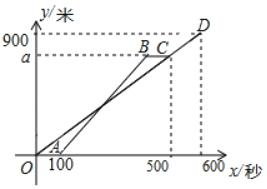
查看答案和解析>>【题目】小明和小亮两人从甲地出发,沿相同的线路跑向乙地,小明先跑一段路程后,小亮开始出发,当小亮超过小明150米时,小亮停在此地等候小明,两人相遇后,两人一起以小明原来的速度跑向乙地,如图是小明、小亮两人在跑步的全过程中经过的路程y(米)与小明出发的时间x(秒)的函数图象,请根据题意解答下列问题:
(1)在跑步的全过程中,小明共跑了 米,小明的速度为 米/秒.
(2)求小亮跑步的速度及小亮在途中等候小明的时间;
(3)求小亮出发多长时间第一次与小明相遇?
相关试题

