【题目】等腰三角形有如下性质:“在等腰三角形中,等边对等角”.即:如图1,在△ABC中,若AB=AC,则∠B=∠C.利用此性质解决以下问题:
如图2,在四边形ABCD中,AD∥BC,点E在边AD上,且CB=CE,点F是射线ED上的一个动点,∠ECF的平分线CG交BE的延长线于点G.
(1)若∠EBC=68°,∠ECF=40°,求G的度数;
(2)在动点F运动的过程中,∠G:∠EFC的值是否发生变化?若不变,求它的值;若变化,请说明理由.

参考答案:
【答案】(1)48°;(2)不变,值为![]()
【解析】
(1)根据∠CEB=∠G+∠GCE,求出∠CEB,∠GCE即可解决问题;
(2)只要证明∠G=![]() ∠EFC即可解决问题.
∠EFC即可解决问题.
解:(1)∵CB=CE,
∴∠CEB=∠CBE=68°,
∵∠GCE=![]() ∠ECF=20°,∠CEB=∠G+∠GCE,
∠ECF=20°,∠CEB=∠G+∠GCE,
∴∠G=68°﹣20°=48°;
(2)结论:不变,理由如下:
∵AD∥BC,
∴∠AEB=∠CBE=∠CEB,
设∠AEB=∠CEB=x,∠GCE=∠GCF=y,
则有![]() ,
,
可得∠G=![]() ∠EFC,
∠EFC,
∴![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.

(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(﹣1,0)、B(3,0)、C(0,3)三点.

(1)求抛物线的解析式.
(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长.
(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四种说法:
①负数的立方根仍为负数;
②1的平方根与立方根都是1;
③4的平方根的立方根是 ;
;
④互为相反数的两个数的立方根仍为相反数,
正确的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
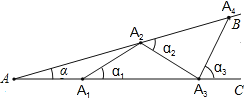
查看答案和解析>>【题目】如图所示,设∠BAC=α(0°
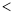 α
α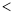 90°),现把等长的小棒依次向右摆放在两射线之间,并使小棒两端分别落在射线AB,AC上,从点A1开始,其中A1A2为第一根小棒,且A1A2=AA1.
90°),现把等长的小棒依次向右摆放在两射线之间,并使小棒两端分别落在射线AB,AC上,从点A1开始,其中A1A2为第一根小棒,且A1A2=AA1.(1)若已经摆放了3根小棒,则∠α1= ;∠α2= ;(用含α的式子表示),若A4A3C=92°,求∠BAC的度数.
(2)若只能摆放6根小棒,求α的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=AC,点D,E分别在直线AB,AC上,且∠DEC=∠DCE
(1)如图1,点D在线段AB上∠A=90°,若等腰直角三角形的边与斜边之比为
 ,求证:
,求证:
(2)如图2,若点D在线段AB的延长线上,∠A=60°,求证:EB=AD

-
科目: 来源: 题型:
查看答案和解析>>【题目】当ab>0时,y=ax2与y=ax+b的图象大致是( )
A.
B.
C.
D.
相关试题

