【题目】下列四种说法:
①负数的立方根仍为负数;
②1的平方根与立方根都是1;
③4的平方根的立方根是 ![]() ;
;
④互为相反数的两个数的立方根仍为相反数,
正确的有( )
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】B
【解析】解:①负数的立方根仍为负数,正确;②1的平方根与立方根都是1,错误; ③4的平方根的立方根是 ![]() ,错误; ④互为相反数的两个数的立方根一定为相反数,正确,所以答案是:B
,错误; ④互为相反数的两个数的立方根一定为相反数,正确,所以答案是:B
【考点精析】关于本题考查的相反数和平方根的基础,需要了解只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;相反数的和为0;a+b=0 :a、b互为相反数;如果一个数的平方等于a,那么这个数就叫做a的平方根(或二次方跟);一个数有两个平方根,他们互为相反数;零的平方根是零;负数没有平方根才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高中学生身体素质,学校开设了A:篮球、B:足球、C:跳绳、D:羽毛球四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校随机抽取若干名学生进行问卷调查(每个被调查的对象必须选择而且只能在四种体育活动中选择一种),将数据进行整理并绘制成以下两幅统计图(未画完整).
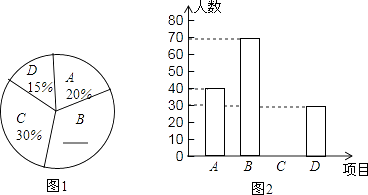
(1)这次调查中,一共调查了名学生;
(2)请补全两幅统计图;
(3)若有3名喜欢跳绳的学生,1名喜欢足球的学生组队外出参加一次联谊活动,欲从中选出2人担任组长(不分正副),求一人是喜欢跳绳、一人是喜欢足球的学生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.

(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(﹣1,0)、B(3,0)、C(0,3)三点.

(1)求抛物线的解析式.
(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长.
(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形有如下性质:“在等腰三角形中,等边对等角”.即:如图1,在△ABC中,若AB=AC,则∠B=∠C.利用此性质解决以下问题:
如图2,在四边形ABCD中,AD∥BC,点E在边AD上,且CB=CE,点F是射线ED上的一个动点,∠ECF的平分线CG交BE的延长线于点G.
(1)若∠EBC=68°,∠ECF=40°,求G的度数;
(2)在动点F运动的过程中,∠G:∠EFC的值是否发生变化?若不变,求它的值;若变化,请说明理由.

-
科目: 来源: 题型:
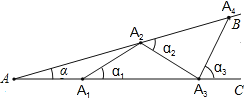
查看答案和解析>>【题目】如图所示,设∠BAC=α(0°
 α
α 90°),现把等长的小棒依次向右摆放在两射线之间,并使小棒两端分别落在射线AB,AC上,从点A1开始,其中A1A2为第一根小棒,且A1A2=AA1.
90°),现把等长的小棒依次向右摆放在两射线之间,并使小棒两端分别落在射线AB,AC上,从点A1开始,其中A1A2为第一根小棒,且A1A2=AA1.(1)若已经摆放了3根小棒,则∠α1= ;∠α2= ;(用含α的式子表示),若A4A3C=92°,求∠BAC的度数.
(2)若只能摆放6根小棒,求α的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=AC,点D,E分别在直线AB,AC上,且∠DEC=∠DCE
(1)如图1,点D在线段AB上∠A=90°,若等腰直角三角形的边与斜边之比为
 ,求证:
,求证:
(2)如图2,若点D在线段AB的延长线上,∠A=60°,求证:EB=AD

相关试题

