【题目】经市场调研发现:某品牌童装平均每天可售出 20 件,每件盈利 40元.在每件降价幅度不超过 18 元的情况下,若每件童装降价 1 元,则每天可多售出 2 件,设降价 x 元.
(1)降价 x 元后,每件童装盈利是多少元,每天销售量是多少件;
(2)要想每天销售这种童装盈利 1200 元,那么每件童装应降价多少元?
(3)每天能盈利 1800 元吗?如果能,每件童装应降价多少元?如果不能,请说明理由.
参考答案:
【答案】(1)降价 x 元后,每件童装盈利是(40﹣x)元,每天销售量是(20+2x)件;(2)每件童装降价 10 元;(3)不能,理由见解析.
【解析】
(1)根据每件童装降价 1 元,每天可多售出 2 件,即可表示出每天的销售数量,
(2)根据总利润=单件利润![]() 销售数量,列出一元二次方程,求解即可,
销售数量,列出一元二次方程,求解即可,
(3)列方程表示出根的判别式即可解题.
(1)降价 x 元后,每件童装盈利是(40﹣x)元,每天销售量是(20+2x)件;
(2)依题意得:(40﹣x)(20+2x)=1200,解得:x1=10,x2=20(舍去),
答:每件童装降价 10 元;
(3)不能,理由如下:
依题意得:(40﹣x)(20+2x)=1800,即:x2﹣30x+500=0,
∵△=302﹣4×1×500=900﹣2000=﹣1100<0,
∴原方程无解,
∴每天销售这种童装不可能盈利 1800 元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 已知反比例函数
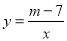 的图象的一支位于第一象限.
的图象的一支位于第一象限.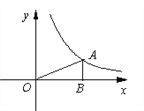
(1)该函数图象的另一分支位于第_____象限,m的取值范围是____________;
(2)已知点A在反比例函数图象上,AB⊥x轴于点B,△AOB的面积为3,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于正数
 ,规定
,规定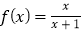 .
.例如:
 ,
, ,
, .
.(1)求值:
 =________ ;
=________ ; __________
__________(2)猜想:
 =___________ ,并证明你的结论;
=___________ ,并证明你的结论;(3)求:
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:①(
 0
0 )-1
)-1 2017
2017 )2018 ; ②
)2018 ; ② a3b2c4)3
a3b2c4)3 2)2;
2)2;③(x+3)(x
 )(x2
)(x2 ) ; ④ 19982+7992+22(用公式计算).
) ; ④ 19982+7992+22(用公式计算).(2)(2a+b)(2ab)(a2b)2+(6a44a2)÷(2a2),其中a=
 ,b=1.
,b=1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=
 (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣
 >0的解集.
>0的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,解答后面的问题:
材料:求代数式x2-2x+5的最小值.
小明同学的解答过程:x2-2x+5=x2-2x+1-1+5=(x-1)2+4
我们把这种解决问题的方法叫做“配方法”.
(1)请按照小明的解题思路,写出完整的解答过程;
(2)请运用“配方法”解决问题:
①若x2+y2-6x+10y+34=0,求y-x的立方根;
②分解因式:4x4+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线CD与直线AB相交于C,根据下列语句画图,并填空.
(1)过点P作PQ∥CD,交AB于点Q(尺规作图);
(2)过点P作PR⊥CD,垂足为R.
(3)在(1)(2)的条件下,若∠ACD=65°,则∠PQB=____度,∠RPQ=____度.

相关试题

