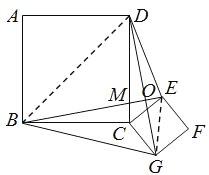
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论有( )

A. 0个 B. 1个 C. 2个 D. 3个
参考答案:
【答案】D
【解析】分析:由四边形ABCD与四边形EFGC都为正方形,得到四条边相等,四个角为直角,利用SAS得到三角形BCE与三角形DCG全等,利用全等三角形对应边相等即可得到BE=DG,利用全等三角形对应角相等得到∠CBM=∠MDO,利用等角的余角相等及直角的定义得到∠BOD为直角,利用勾股定理求出所求式子的值即可.
详解:①∵四边形ABCD和EFGC都为正方形,
∴CB=CD,CE=CG,∠BCD=∠ECG=90°,
∴∠BCD+∠DCE=∠ECG+∠DCE,即∠BCE=∠DCG.
在△BCE和△DCG中,CB=CD,∠BCE=∠DCG,CE=CG,
∴△BCE≌△DCG,
∴BE=DG,
故结论①正确.
②如图所示,设BE交DC于点M,交DG于点O.
由①可知,△BCE≌△DCG,
∴∠CBE=∠CDG,即∠CBM=∠MDO.
又∵∠BMC=∠DMO,∠MCB=180°-∠CBM-∠BMC,∠DOM=180°-∠CDG-∠MDO,
∴∠DOM=∠MCB=90°,
∴BE⊥DG.
故②结论正确.
③如图所示,连接BD、EG,
由②知,BE⊥DG,
则在Rt△ODE中,DE2=OD2+OE2,
在Rt△BOG中,BG2=OG2+OB2,
在Rt△OBD中,BD2=OD2+OB2,
在Rt△OEG中,EG2=OE2+OG2,
∴DE2+BG2=(OD2+OE2)+(OB2+OG2)=(OD2+OB2)+(OE2+OG2)=BD2+EG2.
在Rt△BCD中,BD2=BC2+CD2=2a2,
在Rt△CEG中,EG2=CG2+CE2=2b2,
∴BG2+DE2=2a2+2b2.
故③结论正确.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,中原福塔(河南广播电视塔)是世界第﹣高钢塔.小明所在的课外活动小组在距地面268米高的室外观光层的点D处,测得地面上点B的俯角α为45°,点D到AO的距离DG为10米;从地面上的点B沿BO方向走50米到达点C处,测得塔尖A的仰角β为60°.请你根据以上数据计算塔高AO,并求出计算结果与实际塔高388米之间的误差.(参考数据:
 ≈1.732,
≈1.732,  ≈1.414.结果精确到0.1米)
≈1.414.结果精确到0.1米)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:点P是
 内一点.
内一点.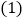 求证:
求证: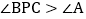 ;
; 若PB平分
若PB平分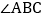 ,PC平分
,PC平分 ,
,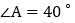 ,求
,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC于D;
(1)如果点F与点A重合,且∠C=50°,∠B=30°,如图1,求∠EFD的度数;
(2)如果点F在线段AE上(不与点A重合),如图2,问∠EFD与∠C﹣∠B有怎样的数量关系?并说明理由.
(3)如果点F在△ABC外部,如图3,此时∠EFD与∠C﹣∠B的数量关系是否会发生变化?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,动点P在∠ABC的平分线BD上,动点M在BC边上,若BC=3,∠ABC=45°,则PM+PC的最小值是( )

A. 2 B.
 C.
C.  D. 3
D. 3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=k1x+2与反比例函数
 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
(1)k1= , k2=;
(2)根据函数图象可知,当y1>y2时,x的取值范围是;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求点P的坐标.
相关试题

