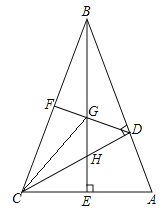
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,连接CG,∠ABE=∠CBE.
(1)求证:BH=AC;
(2)若BG=5,GE=4,求线段AE的长.
参考答案:
【答案】(1)见解析;(2)3.
【解析】
(1)由已知条件易得∠BDC=∠BEC=∠CDA=90°,结合∠ABC=45°,可得∠BCD=∠ABC,由此可得BD=CD,再证得∠DBH=∠DCA即可证得△DBH≌△DCA,由此即可得到BH=AC;
(2)由F是BC的中点,结合(1)中所得BD=CD可得DF是BC的垂直平分线,由此可得BG=CG,结合∠BEC=90°在Rt△CGE中由勾股定理即可求得CE=3,然后再证△ABE≌△CBE,即可得到AE=CE=3.
(1)∵CD⊥AB,BE⊥AC,
∴∠BDC =∠BEC=∠CDA=90°,
∴∠A+∠DCA=90°,∠A+∠ABE=90°,
∴∠ABE=∠DCA,
∵∠ABC=45°,
∴∠BCD=45°=∠ABC,
∴DB=DC,
∵在△DBH和△DCA中,
∵∠DBH=∠DCA,∠BDH=∠CDA,BD=CD,
∴△DBH≌△DCA,
∴BH=AC.
(2)∵F为BC的中点,DB=DC,
∴DF垂直平分BC,
∴CG=BG=5,
∵在Rt△CGE中,∠GEC=90°,CG=5,GE=4,
∴CE=![]() ,
,
∵BE⊥AC,
∴∠BEC=∠BEA=90°,
又∵BE=BE,∠CBE=∠ABE,
∴△ABE≌△CBE,
∴AE=CE=3.
-
科目: 来源: 题型:
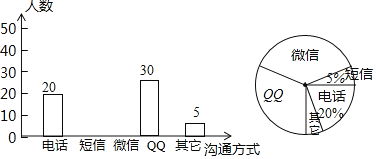
查看答案和解析>>【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样.便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次统计共抽查了_______名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为__________;
(2)某天甲同学想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与乙同学联系,恰好选用“微信”联系的概率为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是由每个边长都是1的小正方形构成的网格,点O,A,B,M均为格点,P为线段OM上的一个动点.

(1)点B到OM的距离等于;
(2)当点P在线段OM上运动,且使PA2+PB2取得最小值时,请借助网格和无刻度的直尺,在给定的网格中画出点P的位置,并简要说明你是怎么画的. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
 与y=m﹣x的图象的一个交点是A(2,3),其中k、m为常数.
与y=m﹣x的图象的一个交点是A(2,3),其中k、m为常数.
(1)求k、m的值,画出函数的草图.
(2)根据图象,确定自变量x的取值范围,使一次函数的函数值大于反比例函数的函数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店准备购进甲,乙两种铅笔,若购进甲种钢笔100支,乙种铅笔50支,需要1000元,若购进甲种钢笔50支,乙种钢笔30支,需要550元.
(1)求购进甲,乙两种钢笔每支各需多少元?
(2)若该文具店准备拿出1000元全部用来购进这两种钢笔,考虑顾客需求,要求购进甲中钢笔的数量不少于乙种钢笔数量的6倍,且不超过乙种钢笔数量的8倍,那么该文具店共有几种.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 在直角坐标系中,
在直角坐标系中, 请写出
请写出 各点的坐标.
各点的坐标. 若把
若把 向上平移2个单位,再向左平移1个单位得到
向上平移2个单位,再向左平移1个单位得到 ,写出
,写出 、
、 、
、 的坐标,并在图中画出平移后图形.
的坐标,并在图中画出平移后图形. 求出三角形ABC的面积.
求出三角形ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】星期天,李玉刚同学随爸爸妈妈会老家探望爷爷奶奶,爸爸8:30骑自行车先走,平均每小时骑行20km;李玉刚同学和妈妈9:30乘公交车后行,公交车平均速度是40km/h.爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同,路程均为40km/h.设爸爸骑行时间为x(h).
(1)请分别写出爸爸的骑行路程y1(km)、李玉刚同学和妈妈的乘车路程y2(km)与x(h)之间的函数解析式,并注明自变量的取值范围;
(2)请在同一个平面直角坐标系中画出(1)中两个函数的图象;
(3)请回答谁先到达老家.
相关试题

