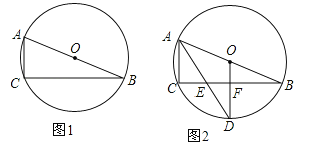
【题目】已知⊙O为△ABC的外接圆,圆心O在AB上.
(1)在图1中,用尺规作图作∠BAC的平分线AD交⊙O于D(保留作图痕迹,不写作法与证明);
(2)如图2,设∠BAC的平分线AD交BC于E,⊙O半径为5,AC=4,连接OD交BC于F.
①求证:OD⊥BC;
②求EF的长.
参考答案:
【答案】(1)作图见试题解析;(2)①证明见试题解析;②![]() .
.
【解析】
试题分析:(1)按照作角平分线的方法作出即可;
(2)①由AD是∠BAC的平分线,得到![]() ,再由垂径定理推论可得到结论;
,再由垂径定理推论可得到结论;
②由勾股定理求得CF的长,然后根据平行线分线段成比例定理求得![]() ,即可求得
,即可求得![]() ,继而求得EF的长.
,继而求得EF的长.
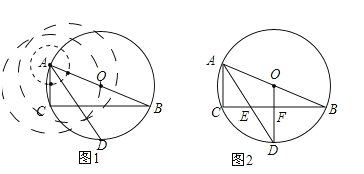
试题解析:(1)尺规作图如图1所示:
(2)①如图2,∵AD平分∠BAC,∴∠DAC=∠BAD,∴![]() , ∵OD过圆心,∴OD⊥CB;
, ∵OD过圆心,∴OD⊥CB;
②∵AB为直径,∴∠C=90°,∵OD⊥CB,∴∠OFB=90°,∴AC∥OD,∴![]() ,,即
,,即![]() ,∴OF=2,∵FD=5﹣2=3,在RT△OFB中,BF=
,∴OF=2,∵FD=5﹣2=3,在RT△OFB中,BF=![]() =
=![]() =
=![]() ,∵OD⊥BC,∴CF=BF=
,∵OD⊥BC,∴CF=BF=![]() ,∵AC∥OD,∴△EFD∽△ECA,∴
,∵AC∥OD,∴△EFD∽△ECA,∴![]() ,∴
,∴![]() ,∴EF=
,∴EF=![]() CF=
CF=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点P(3a,a)是反比例函数y=
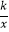 (k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )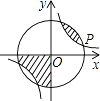
A.y=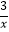
B.y=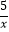
C.y=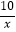
D.y=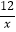
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD内接于⊙O,A是
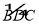 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且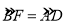 .
.(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.3a2a=6a2
B.(a2)3=a9
C.a6﹣a2=a4
D.3a+5b=8ab -
科目: 来源: 题型:
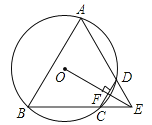
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
(1)求证:∠A=∠AEB;
(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
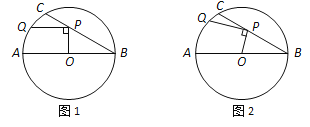
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列成语或词组所描述的事件,不可能事件的是( )
A.守株待兔B.水中捞月C.瓮中捉鳖D.十拿九稳
相关试题

