搜索
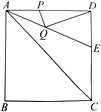
【题目】如图，正方形
的边长是
，
的平分线交
于点
，若点
分别是
和
上的动点，则
的最小值是_______.
参考答案：
【答案】
【解析】
过D作AE的垂线交AE于F，交AC于D′，再过D′作D′P′⊥AD，由角平分线的性质可得出D′是D关于AE的对称点，进而可知D′P′即为DQ+PQ的最小值.
解：解：作D关于AE的对称点D′，再过D′作D′P′⊥AD于P′，
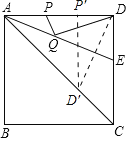
∵DD′⊥AE，
∴∠AFD=∠AFD′，
∵AF=AF，∠DAE=∠CAE，
∴△DAF≌△D′AF，
∴D′是D关于AE的对称点，AD′=AD=5，
∴D′P′即为DQ+PQ的最小值，
∵四边形ABCD是正方形，
∴∠DAD′=45°，
∴AP′=P′D′，
∴在Rt△AP′D′中，
P′D′2+AP′2=AD′2，AD′2=25，
∵AP′=P′D'，
2P′D′2=AD′2，即2P′D′2=25，
，即DQ+PQ的最小值为.
-
科目： 来源： 题型：
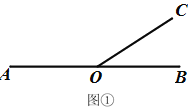
查看答案和解析>>【题目】已知：如图1，点O是直线AB上一点，过点O作射线OC.
(1)若∠AOC=140°，则∠BOC=________°.
(2)在图1中分别画∠AOC的角平分线OE和∠BOC的角平分线OF，那么,OE和OF有什么位置关系，请说明理由.
(3)若∠BOC=30°，射线OD从OB出发，绕点O以每秒10°角的速度逆时针旋转.当射线OD与射线OA重合时，射线OC以每秒30°角的速度绕点O逆时针旋转，射线OD按原来的速度和方向继续旋转，当射线OC或射线OD中有一条射线与射线OB重合时，两条射线都停止.设射线OD旋转的时间为t秒，在旋转的过程中，是否存在某个时刻，使得射线OB、OC与OD中的某一条射线是另两条射线所夹角的平分线?若存在，直接写出所有满足条件的t的值，若不存在，说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】为进一步推进青少年毒品预防教育“627“工程，切实提高广大青少年识毒、防毒、拒毒的意识和能力，我市高度重视全国青少年禁毒知识竞赛活动．针对某校七年级学生的知识竞赛成绩绘制了如图不完整的统计图表．
知识竞赛成绩频数分布表
组别
成绩(分数)
人数
A
95≤x<100
300
B
90≤x<95
a
C
85≤x<90
150
D
80≤x<85
200
E
75≤x<80
b
根据所给信息，解答下列问题．
(1)a＝____，b＝____．
(2)请求出C组所在扇形统计图中的圆心角的度数．
(3)补全知识竞赛成绩频数分布直方图．
(4)已知我市七年级有180000名学生，请估算全市七年级知识竞赛成绩低于80分的人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，抛物线y=x2+（k﹣1）x﹣k与直线y=kx+1交于A、B两点，点A在点B的左侧．
（1）如图1，当k=1时，直接写出A，B两点的坐标；
（2）在（1）的条件下，点P为抛物线上的一个动点，且在直线AB下方，试求出△ABP面积的最大值及此时点P的坐标；
（3）如图2，抛物线y=x2+（k﹣1）x﹣k（k＞0）与x轴交于点C、D两点（点C在点D的左侧），是否存在实数k使得直线y=kx+1与以O、C为直径的圆相切？若存在，请求出k的值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】闵行区政府为残疾人办实事，在道路改造工程中为盲人修建一条长3000米的盲道，根据规划设计和要求，某工程队在实际施工中增加了施工人员，每天修建的盲道比原计划多250米，结果提前2天完成工程，问实际每天修建盲道多少米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】母亲节到了，小明准备为妈妈煮四个大汤圆作早点：一个芝麻馅，一个牛肉馅，两个花生馅，四个汤圆除内部馅料不同外，其它一切均相同．
（1）分别用A，B，C表示芝麻馅、牛肉馅、花生馅的大汤圆，求妈妈吃前两个汤圆刚好都是花生馅的概率（请用“画树状图”或“列表”等方法，写出分析过程，并给出结果）；
（2）若花生馅的大汤圆的个数为n个（n≥2），则妈妈吃前两个汤圆都是花生馅的概率是 （请用含n的式子直接写出结果）
-
科目： 来源： 题型：
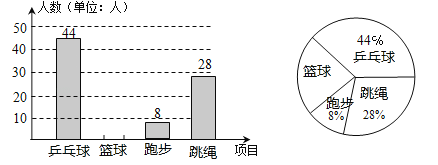
查看答案和解析>>【题目】某校开展“阳光体育”活动，决定开设乒乓球、篮球、跑步、跳绳这四种运动项目，学生只能选择其中一种，为了解学生喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成两张不完整的统计图，请你结合图中的信息解答下列问题：
（1）样本中喜欢篮球项目的人数百分比是 ；其所在扇形统计图中的圆心角的度数是 ；
（2）把条形统计图补画完整并注明人数；
（3）已知该校有1000名学生，根据样本估计全校喜欢乒乓球的人数是多少？
相关试题
