【题目】在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A、B两点,点A在点B的左侧.
(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),是否存在实数k使得直线y=kx+1与以O、C为直径的圆相切?若存在,请求出k的值;若不存在,请说明理由.

参考答案:
【答案】(1)A(﹣1,0),B(2,3)(2)点P坐标为(![]() ,﹣
,﹣![]() )(3)k=
)(3)k=![]() 时,使得直线y=kx+1与以O、C为直径的圆相切
时,使得直线y=kx+1与以O、C为直径的圆相切
【解析】试题分析:(1)当k=1时,联立抛物线与直线的解析式,解方程求得点A、B的坐标;
(2)如图2,作辅助线,求出△ABP面积的表达式,然后利用二次函数的性质求出最大值及点P的坐标;
(3)设以OC为直径的圆与直线AB相切于点Q,由圆周角定理可知,此时![]() 以此为基础,构造相似三角形,利用比例式列出方程,求得k的值.
以此为基础,构造相似三角形,利用比例式列出方程,求得k的值.
试题解析:(1)当k=1时,抛物线解析式为![]() 直线解析式为y=x+1.
直线解析式为y=x+1.
联立两个解析式![]() 得:
得:![]()
解得:x=1或x=2,
当x=1时,y=x+1=0;当x=2时,y=x+1=3,
∴A(1,0),B(2,3).
(2)设![]()
如答图2所示,过点P作PF∥y轴,交直线AB于点F,则F(x,x+1).

∴![]()
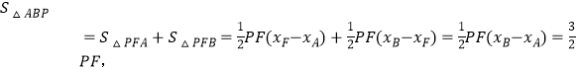
∴![]()
当![]() 时,
时,![]()
∴△ABP面积最大值为![]() ,此时点P坐标为
,此时点P坐标为![]()
(3)设直线AB:y=kx+1与x轴、y轴分别交于点E.F,
则![]()
在Rt△EOF中,由勾股定理得:![]()
令![]() 即(x+k)(x1)=0,解得:x=k或x=1.
即(x+k)(x1)=0,解得:x=k或x=1.
∴C(k,0),OC=k.
设以OC为直径的圆与直线AB相切于点Q,根据圆周角定理,此时![]() 如图3所示,
如图3所示,
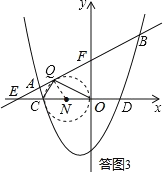
设点N为OC中点,连接NQ,则NQ⊥EF,![]()
∴![]()
∵![]()
∴△EQN∽△EOF,
∴![]() 即:
即: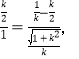
解得:![]()
∵k>0,
∴![]()
即存在实数k使得直线![]() 与以O、C为直径的圆相切.
与以O、C为直径的圆相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,AB=BC=5,∠B=90°,将一块等腰直角三角板的直角顶点O放在斜边AC上,三角板的两直角边分别交直线AB、BC于E、F两点.
(1)如图①,若O为AC的中点,点E、F分别在边AB、BC上.
①当△OFC是等腰直角三角形时,∠FOC= ;
②求证:OE=OF;
(2)如图②,若AO:AC=1:4时,OE和OF有怎样的数量关系?证明你发现的结论.

-
科目: 来源: 题型:
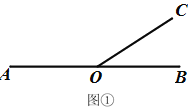
查看答案和解析>>【题目】已知:如图1,点O是直线AB上一点,过点O作射线OC.
(1)若∠AOC=140°,则∠BOC=________°.
(2)在图1中分别画∠AOC的角平分线OE和∠BOC的角平分线OF,那么,OE和OF有什么位置关系,请说明理由.
(3)若∠BOC=30°,射线OD从OB出发,绕点O以每秒10°角的速度逆时针旋转.当射线OD与射线OA重合时,射线OC以每秒30°角的速度绕点O逆时针旋转,射线OD按原来的速度和方向继续旋转,当射线OC或射线OD中有一条射线与射线OB重合时,两条射线都停止.设射线OD旋转的时间为t秒,在旋转的过程中,是否存在某个时刻,使得射线OB、OC与OD中的某一条射线是另两条射线所夹角的平分线?若存在,直接写出所有满足条件的t的值,若不存在,说明理由.
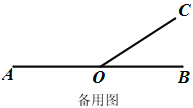
-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步推进青少年毒品预防教育“627“工程,切实提高广大青少年识毒、防毒、拒毒的意识和能力,我市高度重视全国青少年禁毒知识竞赛活动.针对某校七年级学生的知识竞赛成绩绘制了如图不完整的统计图表.

知识竞赛成绩频数分布表
组别
成绩(分数)
人数
A
95≤x<100
300
B
90≤x<95
a
C
85≤x<90
150
D
80≤x<85
200
E
75≤x<80
b
根据所给信息,解答下列问题.
(1)a=____,b=____.
(2)请求出C组所在扇形统计图中的圆心角的度数.
(3)补全知识竞赛成绩频数分布直方图.
(4)已知我市七年级有180000名学生,请估算全市七年级知识竞赛成绩低于80分的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 的边长是
的边长是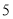 ,
,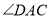 的平分线交
的平分线交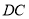 于点
于点 ,若点
,若点 分别是
分别是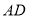 和
和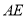 上的动点,则
上的动点,则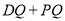 的最小值是_______.
的最小值是_______.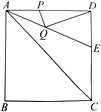
-
科目: 来源: 题型:
查看答案和解析>>【题目】闵行区政府为残疾人办实事,在道路改造工程中为盲人修建一条长3000米的盲道,根据规划设计和要求,某工程队在实际施工中增加了施工人员,每天修建的盲道比原计划多250米,结果提前2天完成工程,问实际每天修建盲道多少米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】母亲节到了,小明准备为妈妈煮四个大汤圆作早点:一个芝麻馅,一个牛肉馅,两个花生馅,四个汤圆除内部馅料不同外,其它一切均相同.
(1)分别用A,B,C表示芝麻馅、牛肉馅、花生馅的大汤圆,求妈妈吃前两个汤圆刚好都是花生馅的概率(请用“画树状图”或“列表”等方法,写出分析过程,并给出结果);
(2)若花生馅的大汤圆的个数为n个(n≥2),则妈妈吃前两个汤圆都是花生馅的概率是 (请用含n的式子直接写出结果)
相关试题

