【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC. 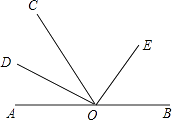
(1)与∠AOE互补的角是 .
(2)若∠AOC=72°,求∠DOE的度数;
(3)当∠AOC=x时,请直接写出∠DOE的度数.
参考答案:
【答案】
(1)∠BOE、∠COE
(2)解:∵OD、OE分别平分∠AOC、∠BOC,∠AOC=72°,
∴∠COD=∠AOD=36°,∠COE=∠BOE= ![]() ∠BOC,
∠BOC,
∴∠BOC=180°﹣72°=108°,
∴∠COE= ![]() ∠BOC=54°,
∠BOC=54°,
∴∠DOE=∠COD+∠COE=90°
(3)解:当∠AOD=x°时,∠DOE=90°
【解析】解:(1)∵OE平分∠BOC,
∴∠BOE=∠COE;
∵∠AOE+∠BOE=180°,
∴∠AOE+∠COE=180°,
∴与∠AOE互补的角是∠BOE、∠COE;
所以答案是∠BOE、∠COE;
【考点精析】本题主要考查了余角和补角的特征的相关知识点,需要掌握互余、互补是指两个角的数量关系,与两个角的位置无关才能正确解答此题.
-
科目: 来源: 题型:
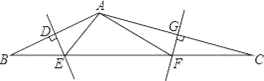
查看答案和解析>>【题目】如图,在△ABC中,AB、AC的垂直平分线分别交BC于点E、F.
(1)若△AEF的周长为10cm,则BC的长为______cm.
(2)若∠EAF=100°,则∠BAC______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把“垂直于同一条直线的两条直线平行”改写成“如果……那么……”的形式是_________________
-
科目: 来源: 题型:
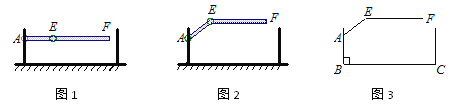
查看答案和解析>>【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC, EF∥BC,∠AEF=143°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37° ≈ 0.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75)
-
科目: 来源: 题型:
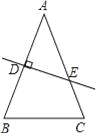
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=32cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.(1)若∠C=70°,则∠BEC=______度;(2)若BC=21cm,则△BCE的周长是______cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0.

(1)求A、B两点的坐标;
(2)点C在数轴上对应的数为x,且x是方程2x+1= x﹣8的解
x﹣8的解
①求线段BC的长;
②在数轴上是否存在点P,使PA+PB=BC?求出点P对应的数;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2+4x+1=0,配方后的方程是( )
A.(x+2)2=5
B.(x﹣2)2=3
C.(x﹣2)2=5
D.(x+2)2=3
相关试题

