搜索
【题目】已知：如图，在梯形ABCD中，AB∥CD，BC=CD，AD⊥BD，E为AB中点，求证：四边形BCDE是菱形． 
参考答案：
【答案】证明：∵AD⊥BD， ∴△ABD是Rt△
∵E是AB的中点，
∴BE= 
AB，DE= AB （直角三角形斜边上的中线等于斜边的一半），
∴BE=DE，
∴∠EDB=∠EBD，
∵CB=CD，
∴∠CDB=∠CBD，
∵AB∥CD，
∴∠EBD=∠CDB，
∴∠EDB=∠EBD=∠CDB=∠CBD，
∵BD=BD，
∴△EBD≌△CBD （ASA ），
∴BE=BC，
∴CB=CD=BE=DE，
∴菱形BCDE．（四边相等的四边形是菱形）
【解析】由题意易得DE=BE，再证四边形BCDE是平行四边形，即证四边形BCDE是菱形．
-
科目： 来源： 题型：
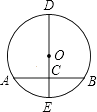
查看答案和解析>>【题目】如图，DE是⊙O的直径，弦AB⊥CD，垂足为C，若AB=6，CE=1，则OC= ， CD= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学为了解本校学生对球类运动的爱好情况，采用抽样的方法，从足球、篮球、排球、其它等四个方面调查了若干名学生，并绘制成“折线统计图”与“扇形统计图”．请你根据图中提供的部分信息解答下列问题：
（1）在这次调查活动中，一共调查了名学生；
（2）“足球”所在扇形的圆心角是度；
（3）补全折线统计图． -
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙、丙三个布袋都不透明，甲袋中装有1个红球和1个白球；乙袋中装有一个红球和2个白球；丙袋中装有2个白球．这些球除颜色外都相同．从这3个袋中各随机地取出1个球． （Ⅰ）取出的3个球恰好是2个红球和1个白球的概率是多少？
（Ⅱ）取出的3个球全是白球的概率是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABO中，已知点
、B（﹣1，﹣1）、O（0，0），正比例函数y=﹣x图象是直线l，直线AC∥x轴交直线l与点C．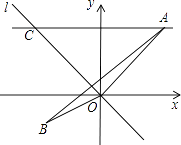 
（1）C点的坐标为；
（2）以点O为旋转中心，将△ABO顺时针旋转角α（90°≤α＜180°），使得点B落在直线l上的对应点为B′，点A的对应点为A′，得到△A′OB′． ①∠α=；②画出△A′OB′．
（3）写出所有满足△DOC∽△AOB的点D的坐标． -
科目： 来源： 题型：
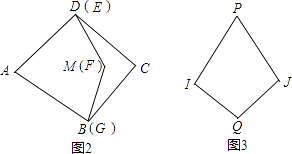
查看答案和解析>>【题目】已知：如图1，图形①满足AD=AB，MD=MB，∠A=72°，∠M=144°．图形②与图形①恰好拼成一个菱形（如图2）．记AB的长度为a，BM的长度为b．
（1）图形①中∠B=°，图形②中∠E=°；
（2）小明有两种纸片各若干张，其中一种纸片的形状及大小与图形①相同，这种纸片称为“风筝一号”；另一种纸片的形状及大小与图形②相同，这种纸片称为“飞镖一号”． ①小明仅用“风筝一号”纸片拼成一个边长为b的正十边形，
需要这种纸片张；
②小明若用若干张“风筝一号”纸片和“飞镖一号”纸片拼成一个“大风筝”（如图3），其中∠P=72°，∠Q=144°，且PI=PJ=a+b，IQ=JQ．请你在图3中画出拼接线并保留画图痕迹．（本题中均为无重叠、无缝隙拼接）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店以6元/千克的价格购进某种干果1140千克，并对其进行筛选分成甲级干果与乙级干果后同时开始销售．这批干果销售结束后，店主从销售统计中发现：甲级干果与乙级干果在销售过程中每天都有销量，且在同一天卖完；甲级干果从开始销售至销售的第x天的总销量y1（千克）与x的关系为y1=﹣x2+40x；乙级干果从开始销售至销售的第t天的总销量y2（千克）与t的关系为y2=at2+bt，且乙级干果的前三天的销售量的情况见下表：
t
1
2
3
y2
21
44
69
（1）求a、b的值；
（2）若甲级干果与乙级干果分别以8元/千克和6元/千克的零售价出售，则卖完这批干果获得的毛利润是多少元？
（3）问从第几天起乙级干果每天的销量比甲级干果每天的销量至少多6千克？ （说明：毛利润=销售总金额﹣进货总金额．这批干果进货至卖完的过程中的损耗忽略不计）
相关试题
