【题目】在数轴上,点A表示数a,点B表示数b,已知a、b满足![]() .
.
(1)求a、b的值;
(2)若在数轴上存在一点C,使得C到A的距离是C到B的距离的2倍,求点C表示的数;
(3)若小蚂蚁甲从点A处以1个单位长度/秒的速度向左运动,同时小蚂蚁乙从点B处以2个单位长度/秒的速度也向左运动,丙同学观察两只小蚂蚁运动,在它们刚开始运动时在原点O处放置一颗饭粒,乙在碰到饭粒后立即背着饭粒以原来的速度向相反的方向运动,设运动的时间为t秒.求甲、乙两只小蚂蚁到原点的距离相等时所对应的时间t.
![]()
参考答案:
【答案】甲、乙两小球到原点的距离相等时经历的时间为![]() 秒或
秒或![]() 秒
秒
【解析】
(1)根据非负数的性质求得a、b的值;
(2)点C可能在A、B之间,也可能在点B的右侧;
(3)需要分类讨论:①甲、乙两球均向左运动,即0≤t≤3时;②甲、乙两球均向左运动,即t>3时.根据速度、时间、距离的关系列出方程并解答.
解:(1)∵![]() ,
,
∴![]() ,
,
解得a=-2,b=6;
(2)设点C表示的数是x,
①当点C在A、B之间时,x-(-2)=2(6-x),
解得x=![]() ;
;
②当点C在B点的右侧时, x-(-2)=2(x-6),
解得x=7
综上所述,点C表示![]() 或7;
或7;
(3)①甲、乙两球均向左运动,即0≤t≤3时,
此时OA=2+t,OB′=6-2t,
则可得方程2+t=6-2t,
解得t=![]() ;
;
②甲继续向左运动,乙向右运动,即t>3时,
此时OA=2+t,OB′=2t-6,
则可得方程2+t=2t-6,
解得t=8.
答:甲、乙两小球到原点的距离相等时经历的时间为![]() 秒或8秒.
秒或8秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c与x轴的一个交点是A(1,0),对称轴为直线x=﹣1,则一元二次方程ax2+bx+c=0的解是 .
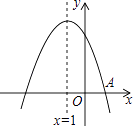
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律:观察下面由“※”组成的图案和算式,解答问题:
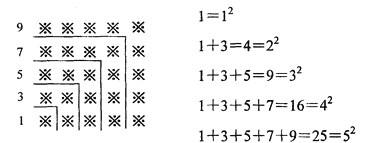
(1)请猜想1+3+5+7+9+…+19=_______________________;
(2)请猜想1+3+5+7+9+…+(2n-1)+(2n+1) =___________;
(3)请用上述规律计算:51+53+55+…+2011+2013.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地果园分别有橘子40吨和60吨,C、D两地分别需要橘子30吨和70吨;已知从A、B到C、D的运价如表:
到C地
到D地
A果园
每吨15元
每吨12元
B果园
每吨10元
每吨9元
(1)若从A果园运到C地的橘子为x吨,则从A果园运到D地的橘子为 ____吨,
从A果园将橘子运往D地的运输费用为 ____ 元.
(2)用含x的式子表示出总运输费(要求:列式、化简).
(3)求总运输费用的最大值和最小值.
(4)若这批橘子在C地和D地进行再加工,经测算,全部橘子加工完毕后总成本为w元,且w=-(x-25)2+4360.则当x= ___ 时,w有最 __ 值(填“大”或“小”).这个值是 __ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司员工分别住在A、B、C三个住宅区,A区有25人,B区有15人,C区有10人,三个区在一条直线上,位置如图所示,公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应设在( )

A. A区 B. B区 C. A区或B区 D. C区
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的一条弦,C是⊙O上一动点且∠ACB=45°,E,F分别是AC,BC的中点,直线EF与⊙O交于点G,H.若⊙O的半径为2,则GE+FH的最大值为 .

-
科目: 来源: 题型:
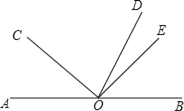
查看答案和解析>>【题目】如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.
(1)若∠AOC=48°,求∠DOE的度数.
(2)若∠AOC=α,则∠DOE= (用含α的代数式表示).
相关试题

