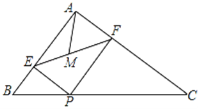
【题目】在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为_____.
参考答案:
【答案】2.4
【解析】
根据已知得当AP⊥BC时,AP最短,同样AM也最短,从而不难根据相似比求得其值.
连结AP,
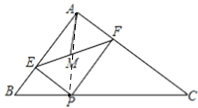
在△ABC中,AB=6,AC=8,BC=10,
∴∠BAC=90°,
∵PE⊥AB,PF⊥AC,
∴四边形AFPE是矩形,
∴EF=AP.
∵M是EF的中点,
∴AM=![]() AP,
AP,
根据直线外一点到直线上任一点的距离,垂线段最短,即AP⊥BC时,AP最短,同样AM也最短,
∴当AP⊥BC时,△ABP∽△CAB,
∴AP:AC=AB:BC,
∴AP:8=6:10,
∴AP最短时,AP=4.8,
∴当AM最短时,AM=AP÷2=2.4.
故答案为2.4
-
科目: 来源: 题型:
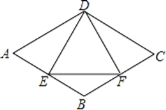
查看答案和解析>>【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )
A.3
B.4
C.1
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 (x>0)的图象交于A(2,﹣1)、B(
(x>0)的图象交于A(2,﹣1)、B( ,n)两点.直线y=2与y轴交于点C.
,n)两点.直线y=2与y轴交于点C.1)求一次函数与反比例函数的解析式;
2)求△ABC的面积;
3)直接写出不等式kx+b>
 在如图所示范围内的解集.
在如图所示范围内的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个直角三角形的直角顶点重合,∠AOC=40°,求∠BOD 的度数.
结合图形,完成填空:
解法 1:
因为
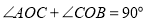 ,
,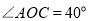
所以
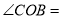
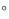
因为

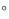
所以
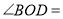
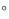
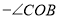
所以
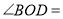
解法2:
因为
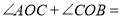
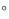 ,
,
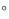 ,①
,①所以
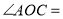 .②
.②因为
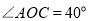
所以
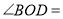
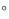
在上面①到②的推导过程中,理由依据是: .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的2017年11月份的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )
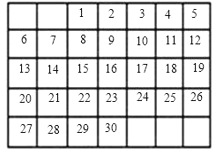
A.27B.51
C.69D.72
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠A=90°,AC=12,点O在AC上,且AO=3,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转90°得到线段OD,要使点D恰好落在BC边上,则OP的长等于( )
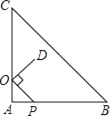
A. 5 B. 3
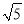 C. 3
C. 3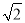 D. 3
D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线y=﹣x(x﹣5)(0≤x≤5),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,得到一“波浪线”,若点P(2018,m)在此“波浪线”上,则m的值为_____.
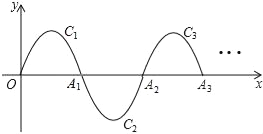
相关试题

