【题目】阅读材料:
关于![]() ,
,![]() 的二元一次方程
的二元一次方程![]() 有一组整数解
有一组整数解![]() 则方程
则方程![]() 的全部整数解可表示为
的全部整数解可表示为![]() (
(![]() 为整数).
为整数).
问题:求方程![]() 的所有正整数解.
的所有正整数解.
小明参考阅读材料,解决该问题如下:
解:该方程一组整数解为![]() 则全部整数解可表示为
则全部整数解可表示为![]() (
(![]() 为整数).
为整数).
因为![]() 解得
解得![]() .因为
.因为![]() 为整数,所以
为整数,所以![]() 0或
0或![]() .
.
所以该方程的正整数解为![]() 和
和![]() .
.
请你参考小明的解题方法, 完成下面的问题:
(1)方程![]() 的全部正整数解为______________;
的全部正整数解为______________;
(2)方程![]() 的全部整数解表示为:
的全部整数解表示为: ![]() (
(![]() 为整数);
为整数);
(3)方程![]() 的正整数解有多少组? 请说明理由.
的正整数解有多少组? 请说明理由.
参考答案:
【答案】(1)![]() 或
或![]() 或
或![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)按材料方法计算即可;
(2)根据![]() 有一组整数解
有一组整数解![]() 则方程
则方程![]() 的全部整数解可表示为
的全部整数解可表示为![]() (
(![]() 为整数)可得;
为整数)可得;
(3)根据材料方法,求得t的取值范围,则t取整数的个数即为方程解的个数.
试题解析:
(1)![]() 的一组整数解为
的一组整数解为![]() 则全部整数解可表示为
则全部整数解可表示为![]() (
(![]() 为整数)
为整数)
因为![]() 解得
解得![]() .因为
.因为![]() 为整数,所以
为整数,所以![]() -2或
-2或![]() .
.
所以该方程的正整数解为![]() 和
和![]() 或
或![]()
(2)∵![]() 的全部整数解表示为:
的全部整数解表示为:![]() (
(![]() 为整数);
为整数);
所以其中这组整数解x=2则y=-1,
所以![]() =-1.
=-1.
(3)![]() 的一组整数解为
的一组整数解为![]() 则全部整数解可表示为
则全部整数解可表示为![]() (
(![]() 为整数)
为整数)
因为![]() 解得
解得![]()
![]() .因为
.因为![]() 为整数,所以
为整数,所以![]() 取整数解的个数共计13个,所以方程
取整数解的个数共计13个,所以方程![]() 的正整数解有13组.
的正整数解有13组.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店进行店庆活动,决定购进甲、乙两种纪念品,若购进甲种纪念品1件,乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需要280元.
(1)购进甲乙两种纪念品每件各需要多少元?
(2)该商场决定购进甲乙两种纪念品100件,并且考虑市场需求和资金周转,用于购买这些纪念品的资金不少于6300元,同时又不能超过6430元,则该商场共有几种进货方案?
(3)若销售每件甲种纪念品可获利30元,每件乙种纪念品可获利12元,在第(2)问中的各种进货方案中,哪种方案获利最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】人们在长期的数学实践中总结了许多解决数学问题的方法,形成了许多光辉的数学想法,其中转化思想是中学教学中最活跃,最实用,也是最重要的数学思想,例如将不规则图形转化为规则图形就是研究图形问题比较常用的一种方法。
问题提出:求边长分别为
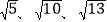 的三角形面积。
的三角形面积。问题解决:在解答这个问题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为
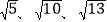 的格点三角形△ABC(如图①),AB=
的格点三角形△ABC(如图①),AB= 是直角边为1和2的直角三角形斜边,BC=
是直角边为1和2的直角三角形斜边,BC=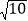 是直角边分别为1和3的直角三角形的斜边,AC=
是直角边分别为1和3的直角三角形的斜边,AC= 是直角边分别为2和3 的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求△ABC的高,而借用网格就能计算出它的面积。
是直角边分别为2和3 的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求△ABC的高,而借用网格就能计算出它的面积。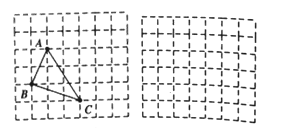
(1)请直接写出图①中△ABC的面积为_______________ 。
(2)类比迁移:求边长分别为
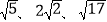 的三角形面积(请利用图②的正方形网格画出相应的△ABC,并求出它的面积)。
的三角形面积(请利用图②的正方形网格画出相应的△ABC,并求出它的面积)。 -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程组解应用题:某学校在筹建数学实验室过程中,准备购进一批桌椅,现有三种桌椅可供选择:甲种每套150元,乙种每套210元,丙种每套250元。若该学校同时购买其中两种不同型号的桌椅50套,恰好花费了9000元,则共有哪几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读再解答:我们已经知道,根据几何图形的面积关系可以说明完全平方公式,实际上还有一些等式也可以用这种方式加以说明,例如:
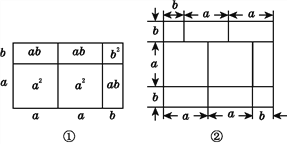
(2a+b)(a+b)=2a2+3ab+b2,就可以用图①的面积关系来说明.
(1)根据图②写出一个等式: ;
(2)已知等式:(x+p)(x+q)=x2+(p+q)x+pq,请你画出一个相应的几何图形加以说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知: 两直线
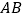 ,
,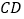 ,且
,且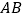 ∥CD,点
∥CD,点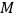 ,
,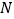 分别在直线
分别在直线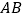 ,
,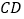 上. 放置一个足够大的三角尺,使得三角尺的两边
上. 放置一个足够大的三角尺,使得三角尺的两边 ,
, 分别经过点
分别经过点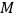 ,
,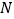 . 过点
. 过点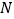 作射线
作射线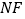 ,使得
,使得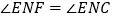 .
. (1)转动三角尺,如图①所示,当射线
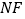 与
与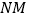 重合,
重合,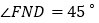 时,则
时,则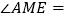 ________;
________;(2)转动三角尺,如图②所示,当射线
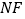 与
与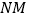 不重合,
不重合, 时,求
时,求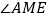 的度数.
的度数. (3)转动直角三角尺的过程中, 请直接写出
 与
与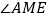 之间的数量关系.
之间的数量关系. 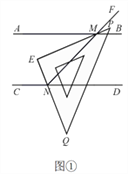


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是小王和小李在一次跑步比赛中的时间和路程图.
(1)这次比赛的路程是_______米;
(2)小王的平均速度是_________米/秒;
(3)他们先到达终点的是_______;
(4)小李跑步的路程
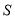 (米)与时间
(米)与时间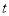 (秒)的函数关系式是_________.
(秒)的函数关系式是_________.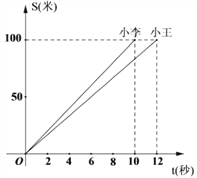
相关试题

