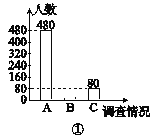
【题目】为了了解初中生毕业后就读普通高中或就读中等职业技术学校的意向,某校对八、九年级部分学生进行了一次调查,调查结果有三种情况:A.只愿意就读普通高中;B.只愿意就读中等职业技术学校;C.就读普通高中或中等职业技术学校都愿意.学校教务处将调查数据进行了整理,并绘制了如图25-3-3所示的尚不完整的统计图,请根据相关信息,解答下列问题:
(1)本次活动共调查了多少名学生?
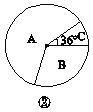
(2)补全图①,并求出图②中B区域的圆心角的度数;
(3)若该校八、九年级的学生共有2800名,请估计该校八、九年级学生中只愿意就读中等职业技术学校的人数.
参考答案:
【答案】(1) 800名学生;(2) 240,补全图形见解析,②中B区域的圆心角的度数是108°;(3)估计该校八、九年级学生中只愿意就读中等职业技术学校的人数为840.
【解析】(1)根据C的人数除以占的百分比,求出调查的学生总数即可;
(2)求出B的人数,补全图1,求出B占的百分比,乘以360即可得到结果;
(3)求出B占的百分比,乘以2800即可得到结果.
解:(1)C部分所占的百分比为![]() ×100%=10%,故本次活动共调查了80÷10%=800(名)学生.
×100%=10%,故本次活动共调查了80÷10%=800(名)学生.
(2)只愿意就读中等职业技术学校的学生人数为800-480-80=240,补全图形如下图所示.图②中B区域的圆心角的度数是![]() ×360°=108°.
×360°=108°.
(3)估计该校八、九年级学生中只愿意就读中等职业技术学校的人数为![]() ×2800=840.
×2800=840.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
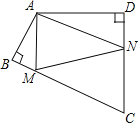
A. 130°B. 120°C. 110°D. 100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】儿童节期间,某公园游戏场举行一场活动.有一种游戏的规则是:在一个装有8个红球和若干白球(每个球除颜色外,其他都相同)的袋中,随机摸一个球,摸到一个红球就得到一个海宝玩具.已知参加这种游戏的儿童有40 000人,公园游戏场发放海宝玩具8 000个.
(1)求参加此次活动得到海宝玩具的频率?
(2)请你估计袋中白球的数量接近多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小红两名同学在学习“概率”时,做掷骰子(质地均匀的正方体)试验.
朝上的点数
1
2
3
4
5
6
出现的次数
7
9
6
8
20
10
(1)她们在一次试验中共掷骰子60次,试验的结果如下:
①填空:此次试验中“5点朝上”的频率为________;
②小红说:“根据试验,出现5点的概率最大.”她的说法正确吗?为什么?
(2)小颖和小红在试验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表法或画树状图法加以说明,并求出其概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 上部分点坐标如表所示,下列说法错误的是( )
上部分点坐标如表所示,下列说法错误的是( )x
…
-3
-2
-1
0
1
…
y
…
-6
0
4
6
6
…
A. 抛物线与y轴的交点为(0,6) B. 抛物线的对称轴是在y轴的右侧;
C. 抛物线一定经过点(3,0) D. 在对称轴左侧,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(-1,0),B(2,-3)两点在一次函数y2=-x+m与二次函数y1=ax2+bx-3的图象上.
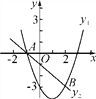
(1)求m的值和二次函数的解析式;
(2)请直接写出使y2>y1时,自变量x的取值范围;
(3)说出所求的抛物线y1=ax2+bx-3可由抛物线y=x2如何平移得到?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,EB=EC,AE的延长线交BC于D,则图中全等的三角形共有_____对.

相关试题

