【题目】为了发展学生的核心素养,培养学生的综合能力,某中学利用“阳光大课间”,组织学生积极参加丰富多彩的课外活动,学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩用下面的折线统计图表示:(甲为实线,乙为虚线)
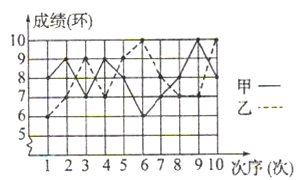
(1)依据折线统计图,得到下面的表格:
射击次序(次) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的成绩(环) | 8 | 9 | 7 | 9 | 8 | 6 | 7 |
| 10 | 8 |
乙的成绩(环) | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 |
| 10 |
其中![]() ________,
________,![]() ________;
________;
(2)甲成绩的众数是________环,乙成绩的中位数是________环;
(3)请运用方差的知识,判断甲、乙两人谁的成绩更为稳定?
(4)该校射击队要参加市组织的射击比赛,已预选出2名男同学和2名女同学,现要从这4名同学中任意选取2名同学参加比赛,请用列表或画树状图法,求出恰好选到1男1女的概率.
参考答案:
【答案】(1)8、7;(2)8,7;(3)甲成绩更稳定;(4)![]()
【解析】![]() 从折线图中得出
从折线图中得出![]() 的值.
的值.
![]() 根据众数,中位数的定义即可求出.
根据众数,中位数的定义即可求出.
![]() 甲乙的射击成绩,再利用方差的公式计算,即可得出答案.
甲乙的射击成绩,再利用方差的公式计算,即可得出答案.
![]() 列表表示出所有的情况,根据概率的求法计算概率.
列表表示出所有的情况,根据概率的求法计算概率.
(1)由折线统计图知a=8、b=7,
故答案为:8、7;
(2)甲射击成绩次数最多的是8环、乙射击成绩次数最多的是7环,
甲成绩的众数是8环、乙成绩的众数为7环;
(3)甲成绩的平均数为![]() =8(环),
=8(环),
所以甲成绩的方差为![]() ×[(6-8)2+2×(7-8)2+4×(8-8)2+2×(9-8)2+(10-8)2]=1.2(环2),
×[(6-8)2+2×(7-8)2+4×(8-8)2+2×(9-8)2+(10-8)2]=1.2(环2),
乙成绩的平均数为![]() =8(环),
=8(环),
所以乙成绩的方差为![]() ×[(6-8)2+4×(7-8)2+(8-8)2+2×(9-8)2+2×(10-8)2]=1.8(环2),
×[(6-8)2+4×(7-8)2+(8-8)2+2×(9-8)2+2×(10-8)2]=1.8(环2),
故甲成绩更稳定;
(4)用A、B表示男生,用a、b表示女生,列表得:
A | B | a | b | |
A | AB | Aa | Ab | |
B | BA | Ba | Bb | |
a | aA | aB | ab | |
b | bA | bB | ba |
∵共有12种等可能的结果,其中一男一女的有8种情况,
∴恰好选到1男1女的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程(组)解应用题:
为顺利通过国家义务教育均衡发展验收,我市某中学配备了两个多媒体教室,购买了笔记本电脑和台式电脑共120台,购买笔记本电脑用了7.2万元,购买台式电脑用了24万元,已知笔记本电脑单价是台式电脑单价的1.5倍,那么笔记本电脑和台式电脑的单价各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
 在反比例函数
在反比例函数 的图象上,过点
的图象上,过点 作
作 轴,垂足为
轴,垂足为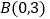 ,直线
,直线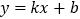 经过点
经过点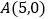 ,与
,与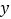 轴交于点
轴交于点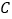 ,且
,且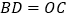 ,
,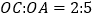 .
.
(1)求反比例函数
 和一次函数
和一次函数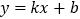 的表达式;
的表达式;(2)直接写出关于
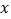 的不等式
的不等式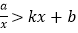 的解集.
的解集. -
科目: 来源: 题型:
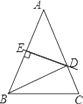
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AB的垂直平分线DE分别交AC、AB于点D、E.
(1)若∠A=46°,求∠CBD的度数;
(2)若AB=8,△CBD周长为13,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1,将矩形纸片
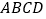 沿对角线
沿对角线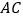 剪开,得到
剪开,得到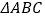 和
和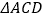 .并且量得
.并且量得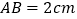 ,
,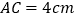 .
.操作发现:
(1)将图1中的
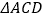 以点
以点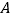 为旋转中心,按逆时针方向旋转
为旋转中心,按逆时针方向旋转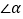 ,使
,使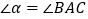 ,得到如图2所示的
,得到如图2所示的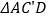 ,过点
,过点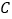 作
作 的平行线,与
的平行线,与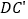 的延长线交于点
的延长线交于点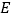 ,则四边形
,则四边形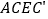 的形状是________.
的形状是________.(2)创新小组将图1中的
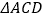 以点
以点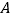 为旋转中心,按逆时针方向旋转,使
为旋转中心,按逆时针方向旋转,使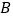 、
、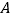 、
、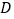 三点在同一条直线上,得到如图3所示的
三点在同一条直线上,得到如图3所示的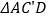 ,连接
,连接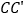 ,取
,取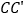 的中点
的中点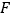 ,连接
,连接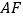 并延长至点
并延长至点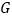 ,使
,使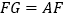 ,连接
,连接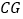 、
、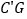 ,得到四边形
,得到四边形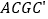 ,发现它是正方形,请你证明这个结论.
,发现它是正方形,请你证明这个结论.实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将
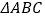 沿着
沿着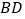 方向平移,使点
方向平移,使点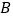 与点
与点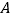 重合,此时
重合,此时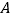 点平移至
点平移至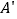 点,
点,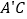 与
与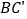 相交于点
相交于点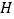 ,如图4所示,连接
,如图4所示,连接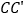 ,试求
,试求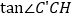 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
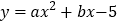 交
交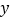 轴于点
轴于点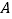 ,交
,交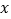 轴于点
轴于点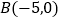 和点
和点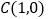 ,过点
,过点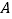 作
作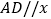 轴交抛物线于点
轴交抛物线于点 .
.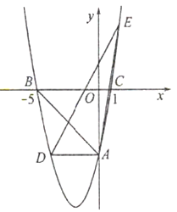
(1)求此抛物线的表达式;
(2)点
 是抛物线上一点,且点
是抛物线上一点,且点 关于
关于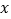 轴的对称点在直线
轴的对称点在直线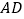 上,求
上,求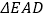 的面积;
的面积;(3)若点
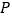 是直线
是直线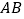 下方的抛物线上一动点,当点
下方的抛物线上一动点,当点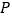 运动到某一位置时,
运动到某一位置时,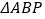 的面积最大,求出此时点
的面积最大,求出此时点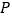 的坐标和
的坐标和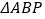 的最大面积.
的最大面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=
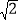 ,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是________.
,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是________.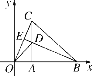
相关试题

