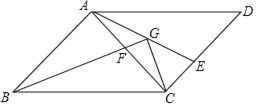
【题目】在平行四边形ABCD中,∠ABC=45°,AB=AC,点E,F分别CD、AC边上的点,且AF=CE,BF的延长线交AE于点G.
(1)若DE=2![]() ,AD=8,求AE.
,AD=8,求AE.
(2)若G是AE的中点,连接CG,求证:![]() AE+CG=BG.
AE+CG=BG.
参考答案:
【答案】(1)2![]() ;(2)详见解析
;(2)详见解析
【解析】
(1)证明△ABC是等腰直角三角形,得出CD=AB=AC=![]() BC=4
BC=4![]() ,求出CE=CD-DE=2
,求出CE=CD-DE=2![]() ,由勾股定理即可得出答案;
,由勾股定理即可得出答案;
(2)证明△ABF≌△CAE(SAS),得出BF=AE,∠ABF=∠CAE,取BF的中点H,连接AH,由直角三角形斜边上的中线性质得出AH=![]() BF=BH,CG=
BF=BH,CG=![]() AE=AG,得出∠ABF=∠BAH,证出∠BAH=∠CAE,证出∠GAH=∠BAF=90°,得出AH=AG=BH=CG,因此△GAH是等腰直角三角形,得出GH=
AE=AG,得出∠ABF=∠BAH,证出∠BAH=∠CAE,证出∠GAH=∠BAF=90°,得出AH=AG=BH=CG,因此△GAH是等腰直角三角形,得出GH=![]() AG=
AG=![]() AE,即可得出结论.
AE,即可得出结论.
(1)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC=8,
∵∠ABC=45°,AB=AC,
∴∠ACB=∠ABC=45°,
∴ACD=∠BAC=90°,
∴△ABC是等腰直角三角形,
∴CD=AB=AC=![]() BC=4
BC=4![]() ,
,
∵DE=2![]() ,
,
∴CE=CD﹣DE=2![]() ,
,
∴AE=![]() =
=![]() =2
=2![]() ;
;
(2)证明:在△ABF和△CAE中,
 ,
,
∴△ABF≌△CAE(SAS),
∴BF=AE,∠ABF=∠CAE,
取BF的中点H,连接AH,如图所示:
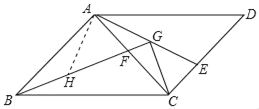
∵∠BAF=90°,AH=![]() BF=BH,
BF=BH,
∴∠ABF=∠BAH,
∴∠BAH=∠CAE,
∴∠GAH=∠BAF=90°,
∵∠ACF=90°,G是AE的中点,
∴CG=![]() AE=AG,
AE=AG,
∴AH=AG=BH=CG,
∴△GAH是等腰直角三角形,
∴GH=![]() AG=
AG=![]() AE,
AE,
∴![]() AE+CG=GH+BH=BG.
AE+CG=GH+BH=BG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年3月15日,我国“两会”落下帷幕.13天时间里,来自各地的5000余名代表、委员聚于国家政治中心,共议国家发展大计.某校初三(3)班张老师为了了解同学们对“两会”知识的知晓情况,进行了一次小测试,测试满分100分.其中
A组同学的测试成绩分别为:91 91 86 93 85 89 89 88 87 91
B组同学的测试成绩分别为:88 97 88 85 86 94 84 83 98 87
根据以上数据,回答下列问题:
(1)完成下表:
组别
平均数
中位数
众数
方差
A组
89
89
b
c
B组
89
a
88
26.2
其中a= ,b= ,c= ,
(2)张老师将B组同学的测试成绩分成四组并绘制成如图所示频数分布直方图(不完整),请补全;
(3)根据以上分析,你认为 组(填“A”或“B”)的同学对今年“两会”知识的知晓情况更好一些,请写出你这样判断的理由(至少写两条):① ② .

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题呈现:我们知道反比例函数y=
 (x>0)的图象是双曲线,那么函数y=
(x>0)的图象是双曲线,那么函数y= +n(k、m、n为常数且k≠0)的图象还是双曲线吗?它与反比例函数y=
+n(k、m、n为常数且k≠0)的图象还是双曲线吗?它与反比例函数y= (x>0)的图象有怎样的关系呢?让我们一起开启探索之旅……
(x>0)的图象有怎样的关系呢?让我们一起开启探索之旅……探索思考:我们可以借鉴以前研究函数的方法,首先探索函数y=
 的图象.
的图象.(1)填写下表,并画出函数y=
 的图象.
的图象.①列表:
x
…
﹣5
﹣3
﹣2
0
1
3
…
y
…
…
②描点并连线.
(2)观察图象,写出该函数图象的两条不同类型的特征:
① ② ;
理解运用:函数y=
 的图象是由函数y=
的图象是由函数y= 的图象向 平移 个单位,其对称中心的坐标为 .
的图象向 平移 个单位,其对称中心的坐标为 .灵活应用:根据上述画函数图象的经验,想一想函数y=
 +2的图象大致位置,并根据图象指出,当x满足 时,y≥3.
+2的图象大致位置,并根据图象指出,当x满足 时,y≥3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年五一期间,重庆洪崖洞民俗风情街景区受热棒,在全国最热门景点中排名第二.许多游客慕名来渝到网红景点打卡,用手机拍摄夜景,记录现实中的“千与千寻”,手机充电宝因此热销.某手机配件店有A型(5000毫安)和B型(10000毫安)两种品牌的充电宝出售
(1)已知A型充电宝进价40元,售价60元,B型充电宝进价60元,要使B型充电宝的利润率不低于A型充电宝的利润率,则B型充电宝的售价至少是多少元(利润率=
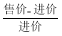 ×100%)
×100%)(2)5月1日,A型充电宝的进价、售价,以及B型充电宝的进价与(1)中相同,B型充电宝按(1)中最低售价出售,其中A型充电宝销量占5月1日总销量的60%.5月2号,A型充电宝进价不变,但销量比5月1号减少
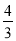 a%,售价提高20元,B型充电宝进价上涨
a%,售价提高20元,B型充电宝进价上涨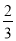 a%,销量增加了
a%,销量增加了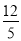 a%,售价在5月1日售价的基础上提高
a%,售价在5月1日售价的基础上提高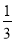 ,结果5月2号的销售利润刚好是5月1号的销售利润的2倍,求a的值.
,结果5月2号的销售利润刚好是5月1号的销售利润的2倍,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】 请阅读下列材料,并解答相应的问题:
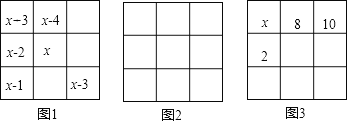
将若干个数组成一个正方形数阵,若任意一行,一列及对角线上的数字之和都相等,则称具有这种性质的数字方阵为“幻方”中国古代称“幻方”为“河图“、“洛书“等,例如,下面是三个三阶幻方,是将数字1,2,3,4,5,6,7,8,9填入到3×3的方格中得到的,其每行、每列、每条对角线上的三个数之和相等.
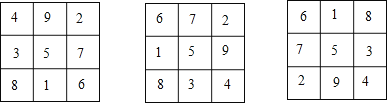
(1)设图1的三阶幻方中间的数字是x,用x的代数式表示幻方中9个数的和为 ;
(2)请你将下列九个数:﹣10、﹣8、﹣6、﹣4、﹣2、0、2、4、6分别填入图2方格中,使得每行、每列、每条对角线上的三个数之和都相等;
(3)图3是一个三阶幻方,那么标有x的方格中所填的数是 ;
(4)如图4所示的每一个圆中分别填写了1、2、3…19中的一个数字(不同的圆中填写的数字各不相同),使得图中每一个横或斜方向的线段上几个圆内的数之和都相等,现在已知该图中七个圆内的数字,则图中的x= ,y= .

-
科目: 来源: 题型:
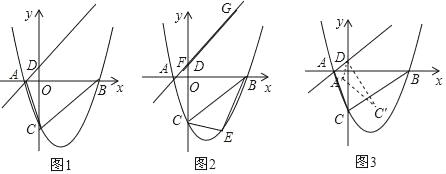
查看答案和解析>>【题目】如图1,抛物线y=
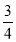 x2﹣
x2﹣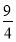 x﹣3,与x轴交于A和B两点(点A在点B的左侧),与y轴交于点C,过点A的直线与抛物线在第一象限的交点M的横坐标为
x﹣3,与x轴交于A和B两点(点A在点B的左侧),与y轴交于点C,过点A的直线与抛物线在第一象限的交点M的横坐标为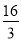 ,直线AM与y轴交于点D,连接BC、AC.
,直线AM与y轴交于点D,连接BC、AC.(1)求直线AD和BC的解折式;
(2)如图2,E为直线BC下方的抛物线上一点,当△BCE的面积最大时,一线段FG=4
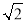 (点F在G的左侧)在直线AM上移动,顺次连接B、E、F、G四点构成四边形BEFG,请求出当四边形BEFG的周长最小时点F的坐标;
(点F在G的左侧)在直线AM上移动,顺次连接B、E、F、G四点构成四边形BEFG,请求出当四边形BEFG的周长最小时点F的坐标;(3)如图3,将△DAC绕点D逆时针旋转角度α(0°<α<180°),记旋转中的三角形为△DA′C′,若直线A′C′分别与直线BC、y轴交于M、N,当△CMN是等腰三角形时,请直接写出CM的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(﹣2,0),B(0,1),以线段AB为边在第二象限作矩形ABCD,双曲线y=
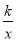 (k<0)过点D,连接BD,若四边形OADB的面积为6,则k的值是( )
(k<0)过点D,连接BD,若四边形OADB的面积为6,则k的值是( )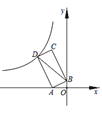
A.﹣9B.﹣12C.﹣16D.﹣18
相关试题

