【题目】如图,一次函数y=mx+1的图象经过点A(﹣1,0),且与反比例函数![]() (k≠0)交于点B(n,2).
(k≠0)交于点B(n,2).
(1)求一次函数的解析式
(2)求反比例函数的解析式
(3)直接写出求当1≤x≤6时,反比例函数y的取值范围.

参考答案:
【答案】(1)y=x+1;(2)y=![]() ;(3)
;(3)![]() ≤y≤2.
≤y≤2.
【解析】试题分析:(1)先把把A(-1,0)代入y=mx+1求m得到一次函数解析式为y=x+1;
(2)根据一次函数解析式确定B点坐标为(1,2),然后把A点坐标代入反比例函数y=![]() ,计算出k即可得到反比例函图象解析式为y=
,计算出k即可得到反比例函图象解析式为y=![]() ;
;
(3) 对于反比例函数,分别计算出x=1和6时的函数值,则可确定反比例函数的取值范围.
试题解析:(1)∵一次函数y=mx+1的图象过点A(﹣1,0),
∴m=1,
∴一次函数的解析式为:y=x+1
(2)把点B(n,2)代入y=x+1,
∴n=1,
把点B的坐标(1,2)代入y=![]() 得:k=2
得:k=2
∴反比例函数解析式为:y=![]() ;
;
(3)当x=1时,y=![]() =2,当x=6时,y=
=2,当x=6时,y=![]() ,
,
所以当1≤x≤6时,反比例函数y的取值范围为![]() ≤y≤2.
≤y≤2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0),…,则点P2018的坐标是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形.
(1)利用尺规作∠ABC的平分线BE,交AD于E(保留作图痕迹,不写作法);
(2)在(1)所作的图形中,求证:AB=AE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AC=5,AB=12,∠BAC的平分线与BC的垂直平分线DG交于点D,DE⊥AC的延长线于点E,DF⊥AB于点F.

(1)求证:CE=BF;
(2)求DG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解全校1800名学生对学校设置的体操、球类、跑步、踢毽子等课外体育活动项目的喜爱情况,在全校范围内随机抽取了若干名学生.对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图所示的频数分布直方图和扇形统计图(均不完整).
(1)补全频数分布直方图;
(2)求扇形统计图中表示“踢毽子”项目扇形圆心角的度数.
(3)估计该校1800名学生中有多少人最喜爱球类活动?

-
科目: 来源: 题型:
查看答案和解析>>【题目】燃放烟花爆竹是中国春节的传统民俗,可注重低碳、环保、健康的市民让今年的烟花爆竹遇冷.在江北区北滨路一烟花爆竹销售点了解到,某种品牌的烟花2013年除夕每箱进价100元,售价250元,销售量40箱 .而2014年除夕当天和去年当天相比,该店的销售量下降了
 %(
%( 为正整数),每箱售价提高了
为正整数),每箱售价提高了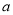 %,成本增加了50%,其销售利润仅为去年当天利润的50%.则
%,成本增加了50%,其销售利润仅为去年当天利润的50%.则 的值为 .
的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是近两周的销售情况:
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
5台
18000元
第二周
4台
10台
31000元
相关试题

