【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE、CD,F为BE的中点,连接AF.
(1)如图①,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.
参考答案:
【答案】
(1)
证明:如图①,
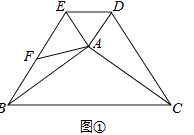
∵∠BAC+∠EAD=180°,∠BAE=90°,
∴∠DAC=90°,
在△ABE与△ACD中
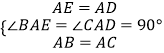
∴△ABE≌△ACD(SAS),
∴CD=BE,
∵在Rt△ABE中,F为BE的中点,
∴BE=2AF,
∴CD=2AF.
(2)
成立,
证明:如图②,
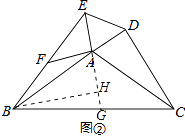
延长EA交BC于G,在AG上截取AH=AD,
∵∠BAC+∠EAD=180°,
∴∠EAB+∠DAC=180°,
∵∠EAB+∠BAH=180°,
∴∠DAC=∠BAH,
在△ABH与△ACD中,
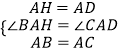
∴△ABH≌△ACD(SAS)
∴BH=DC,
∵AD=AE,AH=AD,
∴AE=AH,
∵EF=FB,
∴BH=2AF,
∴CD=2AF
【解析】(1)因为AF是直角三角形ABE的中线,所以BE=2AF,然后通过△ABE≌△ACD即可求得.(2)延长EA交BC于G,在AG上截取AH=AD,证出△ABH≌△ACD从而证得BH=CD,然后根据三角形的中位线等于底边的一半,求得BH=2AF,即可求得.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则,等等.小学里,把分子比分母小的分数叫做真分数.类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.对于任何一个假分式都可以化成整式与真分式的和的形式, 如:
 =
=  =
=  +
+ 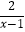 =1+
=1+ 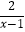 ;
; =
= 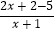 =
=  +
+ 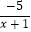 =2+(﹣
=2+(﹣ 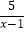 ).
).
(1)下列分式中,属于真分式的是:(填序号); ①
②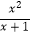
③
④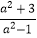
(2)将假分式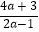 化成整式与真分式的和的形式为:
化成整式与真分式的和的形式为: 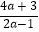 =+ , 若假分式
=+ , 若假分式 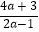 的值为正整数,则整数a的值为;
的值为正整数,则整数a的值为;
(3)将假分式 化成整式与真分式的和的形式:
化成整式与真分式的和的形式:  = .
= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A为某封闭图形边界的一定点,动点P从点A出发,沿其边界顺时针匀速运动一周,设点P的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( ).

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x1 , x2是一元二次方程x2+3x﹣5=0的两个根,则x12x2+x1x22的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若某几何体从某个方向观察得到的视图是正方形,则这个几何体可以是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆锥的主视图是边长为4cm的等边三角形,则该圆锥侧面展开图的面积是cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,菱形ABCD的对角线交于点O,AC=2BD,点P是AO上一个动点,过点P作AC的垂线交菱形的边于M,N两点.设AP=x,△OMN的面积为y, 表示y与x的函数关系的图象大致如图2所示,则菱形的周长为

A. 2 B.
 C. 4 D.
C. 4 D. 
相关试题

