【题目】如图,在Rt△ABC中,∠C=90°,∠ABC=30°,点D是BC边上的点,CD= 3,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,PE+PB的最小值 ______

参考答案:
【答案】9
【解析】
根据翻折变换的性质可得点C、E关于AD对称,再根据轴对称确定最短路线问题,BC与AD的交点D即为使PB+PE的最小值的点P的位置,然后根据∠ABC=30°,求出BD的长,即可求出PE+PB的最小值.
∵将△ACD沿直线AD翻折,点C落在AB边上的点E处,
∴点C、E关于AD对称,
∴点D即为使PB+PE的最小值的点P的位置,PB+PE=BC,
∵∠ABC=30°,
∴BD=2DE=2CD=6,
∴BC=CD+BD=3+6=9.
故答案为:9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如表.与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为x(0<x<0.5).
项目
第一次锻炼
第二次锻炼
步数(步)
10000
①
平均步长(米/步)
0.6
②
距离(米)
6000
7020
注:步数×平均步长=距离.
(1)根据题意完成表格填空;
(2)求x;
(3)王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,量角器的直径与直角三角板ABC的斜边及直角三角板ABD的直角边重合于AB,其中量角器0刻度线的端点与点A重合,点P从A处出发沿AD方向以每秒
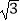 cm的速度移动,CP与量角器的半圆弧交于点E,已知AB=10cm,第5秒时,点E 在量角器上对应的读数是度.
cm的速度移动,CP与量角器的半圆弧交于点E,已知AB=10cm,第5秒时,点E 在量角器上对应的读数是度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.

(1)在给定方格纸中画出平移后的△A′B′C′;
(2)画出AB边上的中线CD和BC边上的高线AE;
(3)线段AA′与线段BB′的关系是: ;
(4) 求四边形ACBB′的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作与思考:一张边长为a的正方形桌面,因为实际需要,需将正方形边长增加b,从而得到一个更大的正方形,木工师傅设计了如图所示的方案:
(1)方案中大正方形的边长都是 ,所以面积为 ;
(2)小明还发现:方案中大正方形的面积还可以用四块小四边形的面积和来表示 ;
(3)你有什么发现,请用数学式子表达 ;
(4)利用(3)的结论计算20.182+2×20.18×19.82+19.822的值.

相关试题

