【题目】如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
(1)求此抛物线的解析式;
(2)在直线AC上有一动点E,当点E在某个位置时,使△BDE的周长最小,求此时E点坐标;
(3)当动点E在直线AC与抛物线围成的封闭线A→C→B→D→A上运动时,是否存在使△BDE为直角三角形的情况,若存在,请直接写出符合要求的E点的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,
∴ ![]() ,
,
∴ ![]() ,
,
∴抛物线解析式为y=x2﹣3x﹣4
(2)
解:如图1,
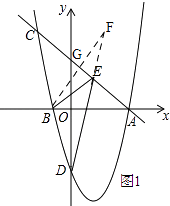
作点B关于直线AC的对称点F,连接DF交AC于点E,
由(1)得,抛物线解析式为y=x2﹣3x﹣4①,
∴D(0,﹣4),
∵点C是直线y=﹣x+4②与抛物线的交点,
∴联立①②解得, ![]() (舍)或
(舍)或 ![]() ,
,
∴C(﹣2,6),
∵A(4,0),
∴直线AC解析式为y=﹣x+4,
∵直线BF⊥AC,且B(﹣1,0),
∴直线BF解析式为y=x+1,
设点F(m,m+1),
∴G( ![]() ,
, ![]() ),
),
∵点G在直线AC上,
∴﹣ ![]() ,
,
∴m=4,
∴F(4,5),
∵D(0,﹣4),
∴直线DF解析式为y= ![]() x﹣4,
x﹣4,
∵直线AC解析式为y=﹣x+4,
∴直线DF和直线AC的交点E( ![]() ,
, ![]() )
)
(3)
解:∵BD= ![]() ,
,
由(2)有,点B到线段AC的距离为BG= ![]() BF=
BF= ![]() ×5
×5 ![]() =
= ![]() >BD,
>BD,
∴∠BED不可能是直角,
∵B(﹣1,0),D(0,﹣4),
∴直线BD解析式为y=﹣4x+4,
∵△BDE为直角三角形,
∴①∠BDE=90°,
∴BE⊥BD交AC于B,
∴直线BE解析式为y= ![]() x+
x+ ![]() ,
,
∵点E在直线AC:y=﹣x+4的图象上,
∴E(3,1),
②∠BDE=90°,
∴BE⊥BD交AC于D,
∴直线BE的解析式为y= ![]() x﹣4,
x﹣4,
∵点E在抛物线y=x2﹣3x﹣4上,
∴直线BE与抛物线的交点为(0,﹣4)和( ![]() ,﹣
,﹣ ![]() ),
),
∴E( ![]() ,﹣
,﹣ ![]() ),
),
即:满足条件的点E的坐标为E(3,1)或( ![]() ,﹣
,﹣ ![]() )
)
【解析】(1)利用待定系数法求出抛物线解析式;(2)先判断出周长最小时BE⊥AC,即作点B关于直线AC的对称点F,连接DF,交AC于点E,联立方程组即可;(3)三角形BDE是直角三角形时,由于BD>BG,因此只有∠DBE=90°或∠BDE=90°,两种情况,利用直线垂直求出点E坐标.此题是二次函数综合题,主要考查了待定系数法,极值,对称性,直角三角形的性质,解本题的关键是求函数图象的交点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,E为CD的中点,H为BE上的一点,
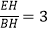 ,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F. 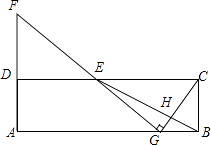
(1)求证: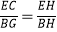 ;
;
(2)若∠CGF=90°,求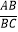 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵桂花树.如图,要求桂花树的位置(视为点P),到花坛的两边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种桂花树的位置点P(不写作法,保留作图痕迹).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列条件中,不能判定直线a与b平行的是( )

A.∠1=∠2
B.∠2=∠3
C.∠3=∠5
D.∠3+∠4=180° -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.(﹣x3)2=x5
B.(﹣3x2)2=6x4
C.(﹣x)﹣2=
D.x8÷x4=x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲
8
9
7
9
8
6
7
8
10
8
乙
6
7
9
7
9
10
8
7
7
10
且
 =8,S乙2=1.8,根据上述信息完成下列问题:
=8,S乙2=1.8,根据上述信息完成下列问题:
(1)将甲运动员的折线统计图补充完整;
(2)乙运动员射击训练成绩的众数是 , 中位数是 .
(3)求甲运动员射击成绩的平均数和方差,并判断甲、乙两人本次射击成绩的稳定性.
相关试题

