【题目】如图,在△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,BG=5,则CF的长为__.

参考答案:
【答案】5
【解析】首先可判断四边形BGFD是平行四边形,再由直角三角形斜边中线等于斜边一半,可得BD=FD,则可判断四边形BGFD是菱形,设GF=x,则AF=13-x,AC=2x,在RT△ACF中利用勾股定理可求出x的值.
∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵GF⊥BD,
∴CF⊥AG,
又∵点D是AC中点,![]() ,
,
∴四边形BGFD是菱形,
设GF=x,则AF=13-x,AC=2x,
∵在RT△ACF中, ∠CFA=90°,
∴AF+CF=AC,即![]() ,
,
解得:x=5,
即BG=5.
故答案是:5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0,
 ),点A坐标为(﹣1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(﹣1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数关系表达式.
(2)点F为线段AC上一动点,过F作FE⊥x轴,FG⊥y轴,垂足分别为E、G,当四边形OEFG为正方形时,求出F点的坐标.
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:数轴上点A表示的数是8,点B表示的数是﹣4.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左运动,动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左运动.P,Q两点同时出发.
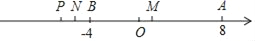
(1)经过多长时间,点P位于点Q左侧2个单位长度?
(2)在点P运动的过程中,若点M是AP的中点,点N是BP的中点,求线段MN的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个自然数的立方,可以分裂成若干个连续奇数的和,例如:23,33和43分别可以按如图所示的方式“分裂”,则63“分裂”出的奇数中,最大的奇数是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA、PB、AB都与⊙O相切,∠P=60°,则∠AOB等于( )
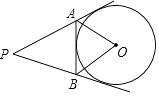
A.50°
B.60°
C.70°
D.70° -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道1+2+3+…+
 =
= ,则1+2+3+…+10= ___________ .
,则1+2+3+…+10= ___________ .[问题提出] 那么
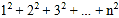 的结果等于多少呢?
的结果等于多少呢?[阅读理解] 在图1所示的三角形数阵中,第1行圆圈中的数为1,即12 ;第2行两个圆圈中数的和为2+2,即22;......;第n行n个圆圈中数的和为n+n+
 n即 n2;这样,该三角形数阵中共有____ 个圆圈,所有圆圈中数的和可表示为_________________ .
n即 n2;这样,该三角形数阵中共有____ 个圆圈,所有圆圈中数的和可表示为_________________ . 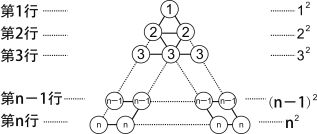
图1
[规律探究] 将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n-1行的第一个圆圈中的数分别为n-1,2,n)发现每个位置上三个圆圈中的数的和均为______________.由此可得,这三个三角形数阵所有圆圈中数的总和为:
3(
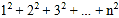 )=_________________.因此,
)=_________________.因此,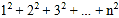 =__________.
=__________. 
图2
[问题解决]
(1).根据以上规律可得
 __________________.
__________________.(2).试计算
 ,请写出计算步骤.
,请写出计算步骤.
相关试题

