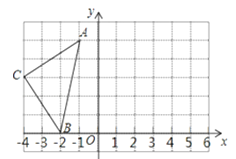
【题目】如图，在平面直角坐标系中，A（﹣1，5），B（﹣2，0），C（﹣4，3）．

（1）请画出△ABC关于y轴对称的△A'B′C′（其中A'、B′、C′分别是A、B、C的对称点，不写画法）；

（2）写出C′的坐标，并求△ABC的面积；

（3）在y轴上找出点P的位置，使线段PA+PB的最小．

参考答案：

【答案】（1）答案见解析；（2）C′的坐标（4，3），6.5；（3）答案见解析．

【解析】试题分析：（1）根据关于y轴对称的点的坐标特点，求出A、B、C的对称点A'、B′、C′,然后描点即可；

（2）利用C′与C关于y轴对称，求出左边，然后根据分割法求出面积；

（3）根据轴对称的性质，和两点之间，线段最短，即可求积P的位置.

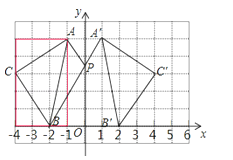
试题解析：解：（1）如图所示：

（2）C′的坐标（4，3），△ABC的面积：3×5﹣0.5×2×3﹣0.5×2×3﹣0.5×1×5=15﹣3﹣3﹣2.5=6.5；

（3）连接A′B，与y轴的交点就是P的位置．

关闭