【题目】一天晚上,身高1.6米的小明站在路灯下,发现自己的影子恰好是4块地砖的长(每块地砖为边长0.5米的正方形).当他沿着影子的方向走了4块地砖时,发现自己的影子恰好是5块地砖的长,根据这个发现,他就算出了路灯的高度,你知道他是怎么算的吗?
参考答案:
【答案】8米
【解析】试题分析:如图,AC=4×0.5m=2m,CE=5×0.5m=2.5m,AB=CD=1.6m,先证明△CAB∽△COP,利用相似比得到![]() ①,再证明△ECD∽△EOP得到
①,再证明△ECD∽△EOP得到![]() ②,然后解关于OP和AO的方程组求出OP即可.
②,然后解关于OP和AO的方程组求出OP即可.
试题解析:如图,AC=4×0.5m=2m,CE=5×0.5m=2.5m,AB=CD=1.6m,
∵AB∥OP,
∴△CAB∽△COP,
∴![]() ,即
,即![]() ①,
①,
∵CD∥OP,
∴△ECD∽△EOP,
∴![]() ,即
,即![]() ②,
②,
由①②得![]() ,解得AO=8,
,解得AO=8,
∴![]() ,解得OP=8.
,解得OP=8.
答:路灯的高度为8m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正多边形的每一个内角都为 135°,则该多边形的边数为( )
A. 5 B. 6 C. 7 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣2,0),C(﹣4,3).
(1)请画出△ABC关于y轴对称的△A'B′C′(其中A'、B′、C′分别是A、B、C的对称点,不写画法);
(2)写出C′的坐标,并求△ABC的面积;
(3)在y轴上找出点P的位置,使线段PA+PB的最小.
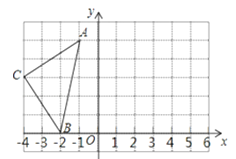
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x2-2x=0 (2)5x(x-1)-3(x-1)=0
(3)x2-10x+9=0 (4)3(x-1)2-27=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,求这块地的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店原来将进货价为8元的商品按10元售出,每天可销售200件.现在采用提高售价,减少进货量的方法来增加利润,已知每件商品涨价1元,每天的销售量就减少20件.设这种商品每个涨价
 元.
元.(1)填空:原来每件商品的利润是 元,涨价后每件商品的实际利润是 元 (可用含
 的代数式表示);
的代数式表示);(2)为了使每天获得700元的利润,售价应定为多少元?
(3)售价定为多少元时,每天利润最大,最大利润是多少元?
相关试题

