【题目】综合:
(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数;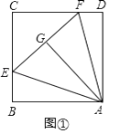
(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN,ND,BM之间的数量关系,并说明理由.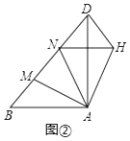
(3)在图①中,连接BD分别交AE,AF于点M,N,若DN=3 ![]() ,BM=3
,BM=3 ![]() ,求MN的长.
,求MN的长.
参考答案:
【答案】
(1)解:如图①,
在Rt△ABE和Rt△AGE中, ![]() ,
,
∴△ABE≌△AGE(HL),
∴∠BAE=∠GAE,
同理∠GAF=∠DAF,
∴∠EAF= ![]() =45°;
=45°;
(2)解:如图②,
∵∠BAD=90°,AB=AD,
∴∠ABD=∠ADB=45°,
由题意知△ABM≌ADH,
∴∠ADH=∠ABM=45°,AH=AM,
∴∠BDH=90°,
∵∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠DAN+∠DAH=45°,
即∠NAH=45°,
在△AMN和△AHN中,
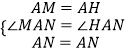 ,
,
∴△AMN≌△AHN(SAS),
∴HN=MN,
在Rt△NDH中,NH2=DH2+ND2,
∴MN2=BM2+DN2
(3)解:如图③,由(2)中结论可知:MN2=BM2+DN2,
∵DN=3 ![]() ,BM=3
,BM=3 ![]() ,
,
∴MN= ![]() =9.
=9.
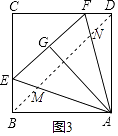
【解析】(1)由HL证明△ABE≌△AGE、△AGF≌△ADF即可,只需证明一对全等,另一对同理可证;(2)先证明△AMN≌△AHN,进而证明△NHD是直角三角形即可;(3)利用(2)中结论建立方程,解之即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解我市市直20000名初中生的身高情况,从中抽取了2000名学生测量身高,在这个问题中,样本容量是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(2a﹣3b)2=(2a+3b)2+N,则表示N的代数式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索函数y=x+
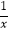 的图象和性质:
的图象和性质:
(1)它的自变量取值范围是;
(2)当x>0时,我们利用列表法画出函数图象
①填写下表,画出函数的图象:x
…



1
2
3
4
…
y
…
…

②观察图象,我们发现函数图象有一个最低点,它的坐标是 ,这说明当x=
,这说明当x=  ,函数y有最小值是
,函数y有最小值是  ;并且,在该点的左边,y随x的增大而
;并且,在该点的左边,y随x的增大而  ,在该点的右边,y随x的增大而
,在该点的右边,y随x的增大而  .
.
③利用上述结论,解决问题:矩形ABCD的面积等于1,当它的长和宽分别为多少时,它的周长最小? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
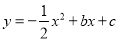 与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.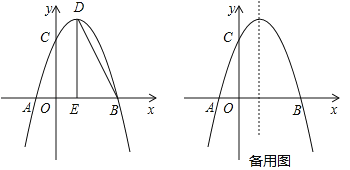
(1)求抛物线的解析式及点D的坐标;
(2)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
(3)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,请写出点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图案中是中心对称图形但不是轴对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前我市人口数约6080000人,用科学记数法表示为_____.
相关试题

