【题目】如图,△ABC中,任意一点P(a,b)经平移后对应点P1(a﹣2,b+3),将△ABC作同样的平移得到△A1B1C1.
(1)求A1,B1,C1的坐标;
(2)指出这一平移的平移方向和平移距离.

参考答案:
【答案】(1)A1(﹣1,4);B1(﹣3,2);C1(2,1);(2)平移的距离为![]() 个单位长度.
个单位长度.
【解析】(1)∵原来点A的坐标为(1,1),B的坐标为(﹣1,﹣1),C的坐标为(4,﹣2),点P(a,b)经平移后对应点P1(a﹣2,b+3),
∴A1(﹣1,4);B1(﹣3,2);C1(2,1);
(2)将△ABC平移得到△A1B1C1,平移的方向是由A到A1的方向,
平移的距离为线段AA1的长度,AA1=![]() ,即平移的距离为
,即平移的距离为![]() 个单位长度.
个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的顶点坐标为A(﹣2,3)B(﹣3,1)C(﹣1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点.
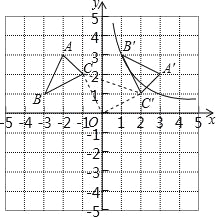
(1)求过点B′的反比例函数解析式;
(2)求线段CC′的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:直线AB∥CD,点E,F分别在直线AB,CD上,点M为平面内一点.
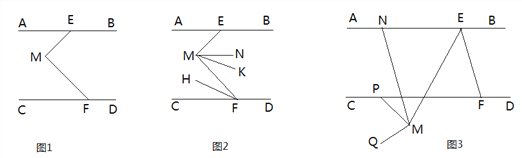
(1)如图1,∠AEM,∠M,∠CFM的数量关系为 ;(直接写出答案)
(2)如图2,∠AEM=48°,MN平分∠EMF,FH平分∠MFC,MK∥FH,求∠NMK的度数;
(3)如图3,点P为CD上一点,∠BEF=n·∠MEF,∠PMQ=n·∠PME,过点M作MN∥EF交AB于点N,请直接写出∠PMQ,∠BEF,∠PMN之间的数量关系.(用含n的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图1,已知Rt△ABC中,AB=BC,AC=2,把一块含30°角的三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),点C在DE上,点B在DF上.
(1)求重叠部分△BCD的面积;
(2)如图2,将直角三角板DEF绕D点按顺时针方向旋转30度,DE交BC于点M,DF交AB于点N.
①求证:DM=DN;
②在此条件下重叠部分的面积会发生变化吗?若发生变化,请求出重叠部分的面积,若不发生变化,请说明理由;
(3)如图3,将直角三角板DEF绕D点按顺时针方向旋转α度(0<α<90),DE交BC于点M,DF交AB于点N,则DM=DN的结论仍成立吗?重叠部分的面积会变吗?(请直接写出结论,不需要说明理由)

-
科目: 来源: 题型:
查看答案和解析>>【题目】每年5月的第二周为:“职业教育活动周”,今年我市展开了以“弘扬工匠精神,打造技能强国”为主题的系列活动,活动期间某职业中学组织全校师生并邀请学生家长和社区居民参加“职教体验观摩”活动,相关职业技术人员进行了现场演示,活动后该校随机抽取了部分学生进行调查:“你最感兴趣的一种职业技能是什么?”并对此进行了统计,绘制了统计图(均不完整).

(1)补全条形统计图和扇形统计图;
(2)若该校共有3000名学生,请估计该校对“工艺设计”最感兴趣的学生有多少人?
(3)要从这些被调查的学生中随机抽取一人进行访谈,那么正好抽到对“机电维修”最感兴趣的学生的概率是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C、D为圆心,大于
 CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是
CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是
A.射线OE是∠AOB的平分线
B.△COD是等腰三角形
C.C、D两点关于OE所在直线对称
D.O、E两点关于CD所在直线对称
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
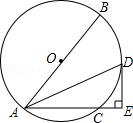
(1)求证:DE是⊙O的切线.
(2)求DE的长.
相关试题

