【题目】如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图: 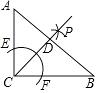
①以C为圆心,以适当长为半径画弧交AC于E,交BC于F.
②分别以E,F为圆心,以大于 ![]() EF的长为半径作弧,两弧相交于P;
EF的长为半径作弧,两弧相交于P;
③作射线CP交AB于点D,
若AC=3,BC=4,则△ACD的面积为 .
参考答案:
【答案】![]()
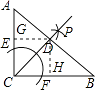
【解析】解:过点D作DG⊥AC,DH⊥BC,垂足分别为G、H,
∵由题意可知CP是∠ACB的平分线,
∴DG=DH.
∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴S△ABC=S△ACD+S△BCD,即 ![]() ×3×4=
×3×4= ![]() ×3DG+
×3DG+ ![]() ×4DG,解得DG=
×4DG,解得DG= ![]() ,
,
∴△ACD的面积= ![]() ×3×
×3× ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】掌握勾股定理的概念是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
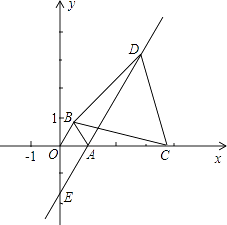
(1)如图,当C点在x轴上运动时,设AC=x,请用x表示线段AD的长;
(2)随着C点的变化,直线AE的位置变化吗?若变化,请说明理由;若不变,请求出直线AE的解析式.
(3)以线段BC为直径作圆,圆心为点F,当点C坐标为多少时直线EF∥直线BO?这时OF和直线BO的位置关系如何?请给予证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】我校开展了“图书节”活动,为了解开展情况,从七年级随机抽取了150名学生对他们每天阅读时间和阅读方式(要求每位学生只能选一种阅读方式)进行了问卷调查,并绘制了如下不完全的统计图
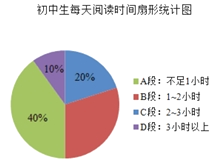
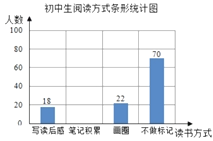
根据上述统计图提供的信息,解答下列问题:
(1)学生每天阅读时间人数最多的是______段,阅读时间在
 段的扇形的圆心角度数是______;
段的扇形的圆心角度数是______;(2)补全条形统计图;
(3)若将写读后感、笔记积累、画圆点读三种方式为有记忆阅读,求笔记积累人数占有记忆阅读人数的百分比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点E、F在线段BD上,AB=CD,∠B=∠D,BF=DE.
求证:(1)AE=CF;(2)AF∥CE.
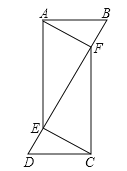
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,AC=BC=6,以A为旋转中心将△ABC顺时针旋转30°得到△ADE,则图中阴影部分的面积= .
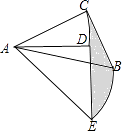
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明乘坐家门口的公共汽车前往西安北站去乘高铁,在行驶了三分之一路程时,小明估计继续乘公共汽车到北站时高铁将正好开出,于是小明下车改乘出租车,车速提高了一倍,结果赶在高铁开车前半小时到达西安北站.已知公共汽车的平均速度是20千米/小时(假设公共汽车及出租车保持匀速行使,途中换乘、红绿灯等待等情况忽略不计),请回答以下两个问题:
(1)出租车的速度为_____千米/小时;
(2)小明家到西安北站有多少千米?
相关试题

