【题目】抛物线y=ax2+bx+c的对称轴是直线x=﹣1,且过点(1,0).顶点位于第二象限,其部分图象如图4所示,给出以下判断:①ab>0且c<0;②4a﹣2b+c>0;③8a+c>0;④c=3a﹣3b;⑤直线y=2x+2与抛物线y=ax2+bx+c两个交点的横坐标分别为x1,x2,则x1+x2+x1x2=5.其中正确的个数有( )
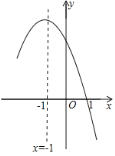
A.5个B.4个C.3个D.2个
参考答案:
【答案】D
【解析】
根据二次函数的图象和性质进行逐一判断即可.
解:∵抛物线对称轴x=﹣1,经过(1,0),
∴![]() =﹣1,a+b+c=0,
=﹣1,a+b+c=0,
∴b=2a,c=﹣3a,
∵a<0,
∴b<0,c>0,
∴ab>0且c>0,故①错误,
∵抛物线对称轴x=﹣1,经过(1,0),
∴(﹣2,0)和(0,0)关于对称轴对称,
∴x=﹣2时,y>0,
∴4a﹣2b+c>0,故②正确,
∵抛物线与x轴交于(﹣3,0),
∴x=﹣4时,y<0,
∴16a﹣4b+c<0,
∵b=2a,
∴16a﹣8a+c<0,即8a+c<0,故③错误,
∵c=﹣3a=3a﹣6a,b=2a,
∴c=3a﹣3b,故④正确,
∵直线y=2x+2与抛物线y=ax2+bx+c两个交点的横坐标分别为x1,x2,
∴方程ax2+(b﹣2)x+c﹣2=0的两个根分别为x1,x2,
∴x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
∴x1+x2+x1x2=![]() +
+![]() =
=![]() +
+![]() =﹣5,故⑤错误,
=﹣5,故⑤错误,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小华设计的“作一个角等于已知角的2倍”的尺规作图过程.
已知:
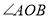 .
.求作:
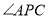 ,使得
,使得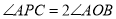 .
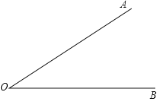
.作法:如图,
①在射线
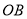 上任取一点
上任取一点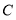 ;
;②作线段
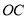 的垂直平分线,交
的垂直平分线,交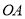 于点
于点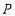 ,交
,交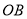 于点
于点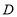 ;
;③连接
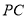 ;
;所以
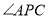 即为所求作的角.
即为所求作的角.根据小华设计的尺规作图过程,
(1)使用直尺和圆规补全图形(保留作图痕迹);
(2)完成下面的证明(说明:括号里填写推理的依据).
证明:∵
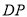 是线段
是线段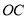 的垂直平分线,
的垂直平分线,∴
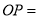 ______(______)
______(______)∴
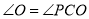 .
.∵
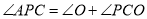 (______)
(______)∴
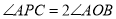 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
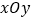 中,直线
中,直线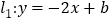 与
与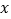 轴,
轴,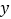 轴分别交于点
轴分别交于点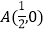 ,B,与反比例函数图象的一个交点为
,B,与反比例函数图象的一个交点为 .
.(1)求反比例函数的表达式;
(2)设直线
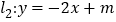 与
与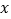
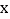 轴,
轴,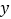 轴分别交于点C,D,且
轴分别交于点C,D,且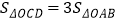 ,直接写出
,直接写出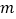 的值 .
的值 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
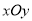 中,已知抛物线
中,已知抛物线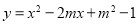 .
.(1)求抛物线的对称轴(用含
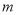 的式子去表示);
的式子去表示);(2)若点
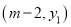 ,
,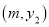 ,
,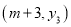 都在抛物线
都在抛物线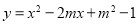 上,则
上,则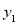 、
、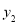 、
、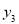 的大小关系为_______;
的大小关系为_______;(3)直线
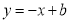 与
与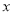 轴交于点
轴交于点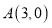 ,与
,与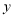 轴交于点
轴交于点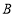 ,过点
,过点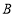 作垂直于
作垂直于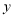 轴的直线
轴的直线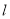 与抛物线
与抛物线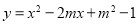 有两个交点,在抛物线对称轴右侧的点记为
有两个交点,在抛物线对称轴右侧的点记为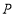 ,当
,当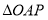 为钝角三角形时,求
为钝角三角形时,求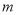 的取值范围.
的取值范围. -
科目: 来源: 题型:
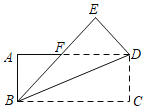
查看答案和解析>>【题目】如图,四边形ABCD是矩形纸片,将△BCD沿BD折叠,得到△BED,BE交AD于点F,AB=3.AF:FD=1:2,则AF=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年9月9日兰州市秦王川国家湿地公园在万众瞩目中盛大开园,公园被分为六大板块,分别为:亲水运动公园、西北戴维营、私人农场区、湿地生态培育区、丝路古镇、湿地科普活动区(分别记为A,B,C,D,E,F),为了了解游客“最喜欢板块”的情况,随机对部分游客进行问卷调查,规定每个人从这六个板块中选择一个,并将调查结果绘制成如下两幅不完整的统计图.

根据以上信息回答下列问题:
(1)这次调查的样本容量是 ,a= ;
(2)扇形统计图中“C”对应的圆心角为 ;
(3)补全条形统计图;
(4)若2019年预计有100000人进园游玩,请估计最喜欢板块为“B”的游客人数.
-
科目: 来源: 题型:
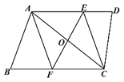
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,点O是对角线AC的中点,过点O作AC的垂线,分别交AD、BC于点E、F,连接AF、CE.试判断四边形AECF的形状,并证明.
相关试题

