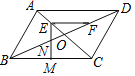
【题目】如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AB=OB,点E、点F分别是OA、OD的中点,连接EF,∠CEF=45°,EM⊥BC于点M,EM交BD于点N,FN=![]() ,则线段BC的长为_____.
,则线段BC的长为_____.
参考答案:
【答案】![]()
【解析】设EF=x,根据三角形的中位线定理表示AD=2x,AD∥EF,可得∠CAD=∠CEF=45°,证明△EMC是等腰直角三角形,则∠CEM=45°,证明△ENF≌△MNB,则EN=MN=![]() x,BN=FN=
x,BN=FN=![]() ,最后利用勾股定理计算x的值,可得BC的长.
,最后利用勾股定理计算x的值,可得BC的长.
设EF=x,
∵点E、点F分别是OA、OD的中点,
∴EF是△OAD的中位线,
∴AD=2x,AD∥EF,
∴∠CAD=∠CEF=45°,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=2x,
∴∠ACB=∠CAD=45°,
∵EM⊥BC,
∴∠EMC=90°,
∴△EMC是等腰直角三角形,
∴∠CEM=45°,
连接BE,
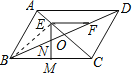
∵AB=OB,AE=OE
∴BE⊥AO
∴∠BEM=45°,
∴BM=EM=MC=x,
∴BM=FE,
易得△ENF≌△MNB,
∴EN=MN=![]() x,BN=FN=
x,BN=FN=![]() ,
,
Rt△BNM中,由勾股定理得:BN2=BM2+MN2,
∴(![]() )2=x2+(
)2=x2+(![]() x)2,
x)2,
x=2![]() 或-2
或-2![]() (舍),
(舍),
∴BC=2x=4![]() .
.
故答案为:4![]() .
.
-
科目: 来源: 题型:
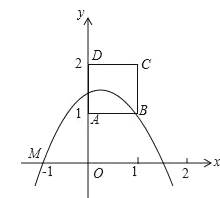
查看答案和解析>>【题目】如图,边长为1的正方形ABCD顶点A(0,1),B(1,1);一抛物线y=ax2+bx+c过点M(﹣1,0)且顶点在正方形ABCD内部(包括在正方形的边上),则a的取值范围是( )
A. ﹣2≤a≤﹣1 B. ﹣2≤a≤﹣
 C. ﹣1≤a≤﹣
C. ﹣1≤a≤﹣ D. ﹣1≤a≤﹣
D. ﹣1≤a≤﹣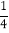
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数
 和
和 (
( 是常数,且
是常数,且 )在同一平面直角坐标系的图象可能是( )
)在同一平面直角坐标系的图象可能是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个等腰直角三角形
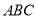 沿斜边上的高
沿斜边上的高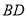 剪下,与剩下部分能拼成一个平行四边形
剪下,与剩下部分能拼成一个平行四边形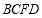 ,如图(1).
,如图(1).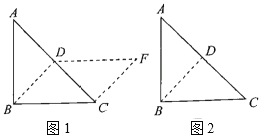
(1)想一想,判断四边形
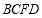 是平行四边形的依据是_____________________________________.(用平行四边形的判定方法叙述)
是平行四边形的依据是_____________________________________.(用平行四边形的判定方法叙述)(2)按上述方法做一做,请你拼一个与图(1)位置或形状不同的平行四边形。并在图(2)中面出示意图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中,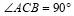 ,
,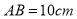 ,
,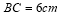 ,若点
,若点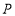 从点
从点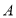 出发以每秒
出发以每秒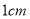 的速度向点
的速度向点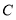 运动,设运动时间为
运动,设运动时间为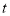 秒
秒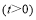 .
.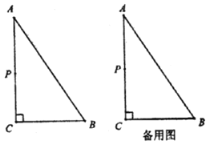
(1)若点
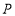 恰好在
恰好在 的角平分线上,求出此时
的角平分线上,求出此时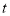 的值;
的值;(2)若点
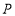 使得
使得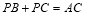 时,求出此时
时,求出此时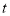 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划销售甲、乙两种产品共
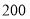 件,每销售
件,每销售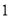 件甲产品可获得利润
件甲产品可获得利润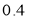 万元, 每销售
万元, 每销售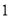 件乙产品可获得利润
件乙产品可获得利润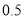 万元,设该商场销售了甲产品
万元,设该商场销售了甲产品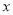 (件),销售甲、乙两种产品获得的总利润为
(件),销售甲、乙两种产品获得的总利润为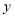 (万元).
(万元).(1)求
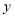 与
与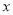 之间的函数表达式;
之间的函数表达式;(2)若每件甲产品成本为
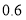 万元,每件乙产品成本为
万元,每件乙产品成本为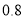 万元,受商场资金影响,该商场能提供的进货资金至多为
万元,受商场资金影响,该商场能提供的进货资金至多为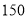 万元,求出该商场销售甲、乙两种产品各为多少件时,能获得最大利润.
万元,求出该商场销售甲、乙两种产品各为多少件时,能获得最大利润.
相关试题

