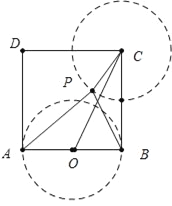
【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.

(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?
②是否存在满足条件的点P,使得PC=![]() ?(不需说明理由).
?(不需说明理由).
参考答案:
【答案】(1)证明见解析;(2)①仍然成立,AP⊥BN和AM=AN. ②这样的点P不存在.
【解析】试题分析:(1)根据相似三角形的性质得到∠PAM=∠PBC,根据正方形的性质证明,得到AP⊥BN,根据相似三角形的对应边的比线段求出AM与AN的数量关系;
(2)①同(1)的证明方法类似;
②根据圆周角定理得到点P在以AB为直径的圆上,根据勾股定理计算即可.
试题解析:(1)如图一中,∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠DAB=∠ABC=∠BCD=∠D=90°,
∵△PBC∽△PAM,∴∠PAM=∠PBC, ![]() ,∴∠PBC+∠PBA=90°,∴∠PAM+∠PBA=90°,
,∴∠PBC+∠PBA=90°,∴∠PAM+∠PBA=90°,
∴∠APB=90°,∴AP⊥BN,∵∠ABP=∠ABN,∠APB=∠BAN=90°,
∴△BAP∽△BNA,∴![]() ,∴
,∴![]() ,∵AB=BC,∴AN=AM.
,∵AB=BC,∴AN=AM.
(2)①仍然成立,AP⊥BN和AM=AN.
理由如图二中,∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠DAB=∠ABC=∠BCD=∠D=90°,
∵△PBC∽△PAM, ∴∠PAM=∠PBC, ![]() ,∴∠PBC+∠PBA=90°,
,∴∠PBC+∠PBA=90°,
∴∠PAM+∠PBA=90°, ∴∠APB=90°,∴AP⊥BN,∵∠ABP=∠ABN,∠APB=∠BAN=90°,
∴△BAP∽△BNA,∴![]() ,∴
,∴![]() ,∵AB=BC,∴AN=AM.
,∵AB=BC,∴AN=AM.
②这样的点P不存在.理由:假设PC=![]() ,如图三中,以点C为圆心
,如图三中,以点C为圆心![]() 为半径画圆,以AB为直径画圆, CO=
为半径画圆,以AB为直径画圆, CO=![]() =
=![]() >1+
>1+![]() ,∴两个圆无公共点,∴∠APB<90°,这与AP⊥PB矛盾,
,∴两个圆无公共点,∴∠APB<90°,这与AP⊥PB矛盾,
∴假设不可能成立,∴满足PC=![]() 的点P不存在.
的点P不存在.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,不是一次函数的是 ( )
A. y=3x B. y=2-x C. y=x D. y=-3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠B=65°,则∠1的度数是( )

A.45°
B.25°
C.20°
D.15° -
科目: 来源: 题型:
查看答案和解析>>【题目】数据共50个,分别落在5个小组内,第一、二、三、四组的数据分别为2、8、15、14,则第五个小组的频数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程x2﹣2x+k=0有两个不相等的实数根,则k的取值范围是( )
A.k<1
B.k>1
C.k<﹣1
D.k>﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】对于命题“如果∠1+∠2=180°,那么∠1≠∠2”,能说明它是假命题的例子是( )
A. ∠1=100°,∠2=80° B. ∠1=50°,∠2=50°
C. ∠1=∠2=90° D. ∠1=80°,∠2=80°
-
科目: 来源: 题型:
查看答案和解析>>【题目】近似数4.50所表示的准确值a的取值范围是( )
A.4.495≤a<4.505
B.4040≤a<4.60
C.4.495≤a≤4.505
D.4.500≤a<4.5056
相关试题

